Alt Küme, özalt küme ve evrensel küme nedir? Alt kümenin ve özalt kümenin özellikleri nelerdir? Alt küme, evrensel küme ile ilgili formüller ve örnekler.
ALT KÜME
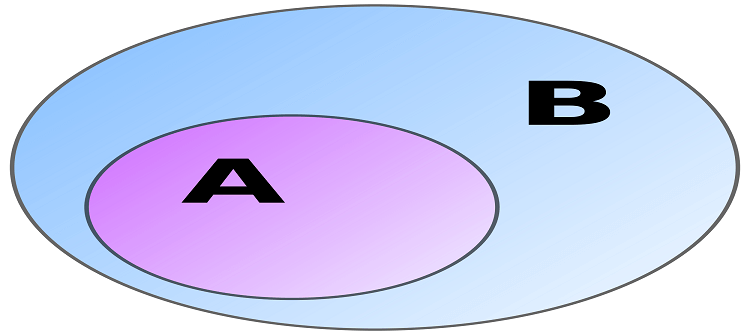
A ve B herhangi iki küme A’nın her elemanı B’ninde bir elemanı ise A kümesine B’nin alt kümesi denir ve A⊂ B şeklinde gösterilir.
ÖRNEK:
- A= {x I -1 ≤ x < 5, x ∈ Z}
- B= {x I -2 ≤ x ≤ 5, x ∈ Z}
- A ve B’yi liste yöntemi ile yazarsak:
- A= {-1,0,1,2,3,4}
- B= {-2, -1,0,1,2,3,4,5}
A’nın her elemanının B’nin bir elemanı olduğu görülür. A ⊂ B dir.
Not: Boş küme her kümenin alt kümesidir.
ÖZALT KÜME
Bir kümenin kendisinden farklı her bir alt kümesine öz alt küme denir.
Not: Eleman sayısı n olan bir kümenin
Alt küme sayısı: 2n
Öz alt küme sayısı: 2n -1
r elemanlı alt kümelerin sayısı:
formülleri ile bulunur.
ÖRNEK:
Altı elemanlı bir kümenin:
a) Alt küme sayısını
b) Öz alt küme sayısını
c) Üçten az elemanlı alt küme sayısını bulunuz.
ÇÖZÜM:
- Alt küme sayısı: 26 = 64
- Öz alt küme sayısı: 64 -1 = 63
- İki elemanlı alt küme sayısı :
- Bir elemanlı alt küme sayısı :
- Sıfır elemanlı alt küme sayısı:
- 3ten az elemanlı alt küme sayısı:
- 15 + 6 + 1 = 22’dir.
Alt Kümenin Özellikleri
Boş küme A kümesinin alt kümesidir
A kümesi kendisinin alt kümesidir
A kümesi B kümesinin alt kümesi ve B kümesi de A kümesinin alt kümesi ise, bu durumda A ve B kümeleri birbirine eşittir.
A kümesi B kümesinin alt kümesi ve B kümesi de C kümesinin alt kümesi ise bu durumda A kümesi C kümesinin alt kümesidir.
- * n elemanlı bir kümenin alt kümeleri sayısı 2n dir
- * Bir kümenin kendisi hariç diğer alt kümelerine bu kümelerin özalt kümeleri denir. n elemanlı bir kümenin özalt kümeleri sayısı 2n – 1 dir.
- * n elemanlı bir kümenin r elemanlı (r ≤ n) alt kümeleri sayısı;
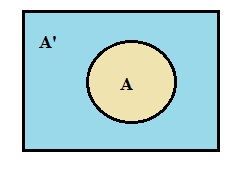
Evrensel Küme
Evrensel Küme: çözülecek probleme göre düşünülen en geniş kümeye evrensel küme denir. Tümleme:
Evrensel kümenin elemanı olupta A kümesinde bulunmayan elemanların oluşturduğu kümeye A’nın tümleyeni denir ve (A’) ile gösterilir.
- A’ = {x I x ∈ E ve x ∉ A}
- Şema ile gösterilirse: