Matematik derslerinde sıkça karşılaşılan üstel fonksiyonlar hakkında derinlemesine bir bilgi edinmek ister misiniz? Bu yazıda, üstel fonksiyonların tanımından türeviden grafiklerine kadar her detayı ele alıyoruz.
Üstel fonksiyonlar, matematikte sıklıkla kullanılan bir tür fonksiyondur. Bir üstel fonksiyon, tabanı bir sabit olan ve bu sabitin üs olarak kullanıldığı bir fonksiyondur. Genel olarak, üstel fonksiyon şu şekilde tanımlanır:
f(x) = a^x
Burada, f(x) üstel fonksiyonun değerini temsil ederken, a tabanı ve x ise bağımsız değişkeni ifade eder. Taban olan a, pozitif bir sabit olmalıdır.
Üstel fonksiyonlar, genellikle matematiksel modellemelerde, büyüme oranları ve değişimleri ifade etmek için kullanılır. Özellikle doğal fenomenlerde, büyüme, bozunma, popülasyon dinamikleri ve maliyet analizleri gibi alanlarda sıkça karşılaşılır. Üstel fonksiyonların bazı özellikleri şunlardır:
- Taban a>0 ve a ≠ 1 olmalıdır. Bu, tabanın pozitif olması ve 1’den farklı olması gerektiği anlamına gelir.
- Üstel fonksiyonun tanım kümesi, tüm gerçek sayıları kapsar.
- Taban a’nın değerine göre, üstel fonksiyon farklı davranışlar gösterebilir. Örneğin, a>1 ise fonksiyon sürekli bir şekilde artar, a<1 ise sürekli bir şekilde azalır ve a=1 ise sabit bir fonksiyon olur.
- Üstel fonksiyonun grafiği, y ekseni üzerinde kesikli bir doğru olan J şeklinde bir eğriye benzer.
- Üstel fonksiyon, pozitif bir tabanın pozitif bir üs kuvvetini hesaplayabilirken, negatif bir tabanın üssü tanımsızdır. Yani, negatif tabanlarla üstel fonksiyon tanımı genellikle yapılmaz.
Üstel fonksiyonlar, matematiksel analizde ve uygulamalı matematikte önemli bir rol oynamaktadır. Doğal logaritma ve üstel denklemler gibi konular, üstel fonksiyonlarla sıkı bir şekilde ilişkilidir.
Üstel fonksiyonların türevini nasıl alırım?
Üstel fonksiyonların türevini almak için aşağıdaki adımları takip edebilirsiniz:
- İlk adım, üstel fonksiyonun tanımını hatırlamaktır. Üstel fonksiyon f(x) = a^x olarak tanımlanır, burada a tabanı ve x bağımsız değişkenidir.
- Üstel fonksiyonun türeviden, doğal logaritma (ln) fonksiyonunun kullanılması gerekmektedir. Doğal logaritma fonksiyonunun türevidir: d/dx(ln(x)) = 1/x.
- Üstel fonksiyonun türevidi almak için, f(x) = a^x ifadesinin her iki tarafını doğal logaritma fonksiyonuna uygularız:
ln(f(x)) = ln(a^x)
- Doğal logaritma fonksiyonunun özelliği olan logaritma ile üstel fonksiyonu ayrıştırma kuralını kullanarak, üstel fonksiyonu çarpanlara ayırabiliriz:
ln(f(x)) = x ln(a)
- Her iki tarafın türevini alarak, üstel fonksiyonun türevidini elde ederiz:
d/dx(ln(f(x))) = d/dx(x ln(a))
- Sol taraftaki türevi hesaplamak için zincir kuralını kullanırız:
1/f(x) * f'(x) = 1 * ln(a)
- f'(x) ifadesini elde etmek için yukarıdaki denklemi f(x) için çözeriz:
f'(x) = f(x) * ln(a)
- İlk adımda verilen üstel fonksiyon tanımını tekrar kullanarak, türevi şu şekilde ifade edebiliriz:
f'(x) = a^x * ln(a)
Bu şekilde üstel fonksiyonun türevidini elde edebilirsiniz. Önemli olan nokta, üstel fonksiyonun türevidinin kendisinin ve doğal logaritmanın birleşimi olduğudur. Bu özellik, üstel fonksiyonların türevini hesaplarken sıklıkla kullanılır.
Üstel fonksiyonların türevini alma
Üstel fonksiyonun türevidini almak için aşağıdaki adımları izleyebilirsiniz:
- İlk adımda, üstel fonksiyonun tanımını hatırlayalım: f(x) = a^x, burada a tabanı ve x bağımsız değişkendir.
- Türev alma kuralına göre, üstel fonksiyonun türevidini almak için tabanı sabit tutarız ve üs kısmını türeveriz.
f'(x) = d/dx(a^x)
- Üstel fonksiyonun türevidini almak için doğal logaritma (ln) kullanacağız. Doğal logaritma fonksiyonunun türevidir: d/dx(ln(x)) = 1/x.
- Dolayısıyla, üstel fonksiyonun türevidini almak için aşağıdaki adımları izleriz:
f'(x) = d/dx(a^x) = d/dx(e^(ln(a^x))) (e, doğal logaritmanın tabanı olan Euler sayısıdır) = d/dx(e^(x * ln(a))) (üstel fonksiyonun tanımını doğal logaritmaya dönüştürdük) = e^(x * ln(a)) * d/dx(x * ln(a)) (zincir kuralını kullanarak türevleri çarparız) = a^x * ln(a)
Sonuç olarak, üstel fonksiyonun türevi f'(x) = a^x * ln(a)’dır. Bu formül, üstel fonksiyonların türevini hesaplamak için kullanılır.
Üstel Fonksiyon Grafiklerinde Dönüşümler
Üstel fonksiyonların grafiklerinde bazı dönüşümler uygulanabilir. İşte yaygın olarak kullanılan üç dönüşüm:
- Yatay Dönüşüm (Shift): Yatay dönüşüm, üstel fonksiyonun grafiklerini sağa veya sola kaydırmak için kullanılır. f(x) = a^(x – h) şeklinde bir yatay dönüşüm yapmak istediğimizde, h değeri yatay kaydırmanın miktarını temsil eder. h değeri pozitif ise fonksiyon sağa kayar, h değeri negatif ise fonksiyon sola kayar.
- Dikey Dönüşüm (Scale): Dikey dönüşüm, üstel fonksiyonun grafiklerini yukarı veya aşağı doğru ölçeklendirmek için kullanılır. f(x) = a^x + k şeklinde bir dikey dönüşüm yapmak istediğimizde, k değeri dikey kaydırmanın miktarını temsil eder. k değeri pozitif ise fonksiyon yukarı doğru kayar, k değeri negatif ise fonksiyon aşağı doğru kayar.
- Yatay ve Dikey Dönüşüm (Shift and Scale): Yatay ve dikey dönüşümleri bir arada kullanarak daha karmaşık dönüşümler yapabiliriz. Örneğin, f(x) = a^(bx + c) şeklinde bir dönüşüm yapmak istediğimizde, b parametresi yatay ölçeklemeyi, c parametresi ise yatay kaydırmayı temsil eder. Bu tür dönüşümler, üstel fonksiyonların grafiklerini çeşitli şekillerde değiştirebilir.
Bu dönüşümler, üstel fonksiyon grafiklerinin konumunu, büyüklüğünü ve şeklini değiştirmek için kullanılır. Grafiklerdeki dönüşümler, fonksiyonun tabanı (a) ve parametre değerlerine bağlı olarak çeşitli sonuçlar üretebilir.
Fonksiyonları Grafiklerle Eşleştirelim
İşte yaygın olarak kullanılan bazı fonksiyonlar ve onların grafikleri:
- Lineer Fonksiyon (f(x) = mx + b): Lineer fonksiyonlar, doğrusal bir ilişkiyi temsil eder. m eğim (eğim katsayısı) ve b y eksenini kestiği noktadaki y değerini ifade eder. Grafikleri düz bir çizgi şeklindedir.

- Kare Fonksiyon (f(x) = x^2): Kare fonksiyon, bağımsız değişkenin karesi ile tanımlanan bir parabolün grafiğini oluşturur. Grafik, simetrik bir U şekline sahiptir ve y ekseni etrafında aynalanır.

- Mutlak Değer Fonksiyonu (f(x) = |x|): Mutlak değer fonksiyonu, bağımsız değişkenin mutlak değerini alarak pozitif bir değer üretir. Grafik, x ekseni üzerinde simetriktir ve y değerleri her zaman pozitiftir.
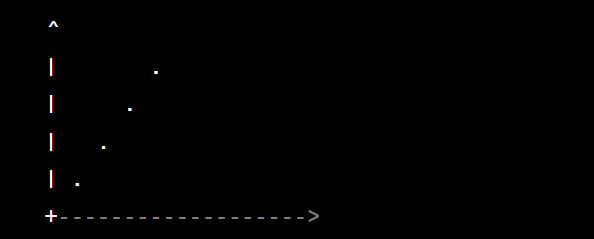
- Üstel Fonksiyon (f(x) = a^x): Üstel fonksiyon, sabit bir tabana (a) sahip olduğunda grafikleri hızla artan veya azalan bir doğruya benzer. Tabanın değerine bağlı olarak farklı büyüme hızları gösterebilir.

- Logaritmik Fonksiyon (f(x) = log_a(x)): Logaritmik fonksiyon, sabit bir tabana (a) sahip olduğunda, grafikleri y ekseni boyunca yavaşça artar veya azalır. Logaritmanın tabanı ve x değeri arasındaki ilişki belirleyici bir faktördür.
Örnek grafik (a > 1):

Tabii ki, bu sadece bazı örneklerdir ve farklı fonksiyonlar için daha farklı grafikler elde edilebilir.