Binom Teoremi Nedir?

Binom teoremi, iki terimli teoremi nedir? Binom teoreminin açıklanması, hesaplanması, hakkında bilgi.

Binom Teoremi

Binom Teoremi; Herhangi bir pozitif n tamsayısı için, iki a ve b sayısının toplamının n’inci kuvvetinin,

$\displaystyle \left( \begin{matrix} n \\ r \\ \end{matrix} \right){{a}^{n-r}}{{b}^{r}}$

biçimindeki n+1 teriminin toplamına eşit olduğunu ifade eden teoremdir. Burada r indisi, sırayla 0, 1, 2, …., n değerlerini alır; ikiterimli katsayıları adı verilen katsayılar ise,

$\displaystyle \left( \begin{matrix} n \\ r \\ \end{matrix} \right)=n!/\left( n-r \right)!r!$

formülü ile verilir; burada n\ (n faktoriyel), l’den n’e kadar tamsayıların çarpımına eşittir. İkiterimli katsayılarının aşağıdaki bağıntılara uyduğu gösterilebilir:

$\displaystyle \left( \begin{matrix} n \\ 0 \\ \end{matrix} \right)=\left( \begin{matrix} n \\ n \\ \end{matrix} \right)=1;$

$\displaystyle \left( \begin{matrix} n \\ r \\ \end{matrix} \right)=\left( \begin{matrix} n \\ n-r \\ \end{matrix} \right)$

Örneğin n=3 için, ikiterimli katsayıları, r=0, 1, 2, 3 alınarak,

$\displaystyle \left( \begin{matrix} 3 \\ 0 \\ \end{matrix} \right)=1;\left( \begin{matrix} 3 \\ 1 \\ \end{matrix} \right)=3;\left( \begin{matrix} 3 \\ 2 \\ \end{matrix} \right)=3;\left( \begin{matrix} 3 \\ 3 \\ \end{matrix} \right)=1$

bulunur. Demek ki n=3 için binom açılımı $\displaystyle {{\left( a+b \right)}^{3}}={{a}^{3}}+3{{a}^{2}}b+3a{{b}^{2}}+{{b}^{3}}$ biçimindedir.

İkiterimli katsayıları, Pascal üçgeni denilen sayılar üçgenindeki sayılara eşittir. Pascal üçgeni 1 sayısı ile başlayan ve iki sayının toplamı bunların arasına ve bir alt satıra yazılarak oluşturulan üçgen biçimli bir diziliştir:

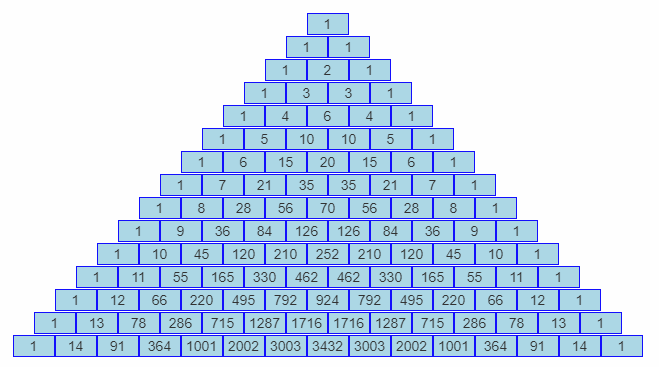
Pascal üçgeninde, en üstteki satır n=0’a, onun altındaki satır n=l’e karşılık gelir ve n büyüdükçe aşağı satırlara geçilir. Her satırda en soldaki sayı r=0’a, onun sağındaki sayı r=l’e karşılık gelir ve r büyüdükçe sağa doğru gidilir. Örneğin

$\displaystyle \left( \begin{matrix} 3 \\ 1 \\ \end{matrix} \right)=3;\left( \begin{matrix} 4 \\ 2 \\ \end{matrix} \right)=6$

Binom teoreminin genel biçimini (herhangi bir n için) ilk kez Isaac Newton 1676’da ortaya koymuş ama kanıt vermemiştir. Binom açılımı bazı basit durumlar için daha önceden de biliniyordu. Teoremi İsviçreli matematikçi Jakob Bernoulli kanıtlamış, bu kanıt Bernoulli’nin ölümünden sonra, 1713’te yayımlanmıştır.