Brown hareketi nedir, nasıl bir harekettir? Brown Hareketinin özellikleri, rassal yürüyüş, difüzyon, fraktallar hakkında bilgi.
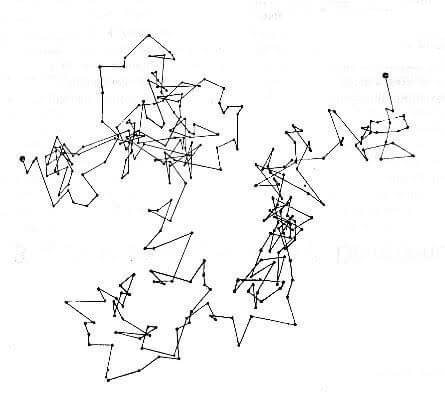
Brown Hareketi
Brown hareketi, bir sıvının veya gazın içindeki çok küçük parçacıkların dört bir yana yaptığı gelişigüzel hareketlerdir. İlk olarak mikroskobunun ıslak lamında hareket eden polenleri gören botanikçi Robert Brown tarafından gözlenmiştir. Hareketi matematiksel olarak açıklayan kişiyse Albert Einstein olmuştur. Brown hareketi, durgun suda veya havada kirliliğin nasıl yayıldığını açıkladığı gibi, su taşkınları veya borsa hareketleri gibi birçok rassal süreci de açıklar. Aynı zamanda fraktalların oluşumunda devreye girer.
19. yüzyıl botanikçilerinden Robert Brown, mikroskobuyla polen tanelerini incelerken onların bulundukları yerde durmak yerine kıpraşarak düzensiz hareketler yaptığını fark etti. Bir an için canlı olabileceklerini düşündüyse de olmadıkları açıktı. Gerçekte polenler Brown’in her zaman hafifçe ıslattığı lamdaki su moleküllerinin hareketleri esnasında kendilerine çarpmasından etkileniyorlardı. Polenler rastgele yönlerde bazen çok kısa, bazen de uzun uzun ilerliyorlardı. Brown’in keşfi birçok biliminsanının aklını karıştırdı ve zamanla Brown’in adıyla anılmaya başlandı.
Rassal yürüyüş
Sudaki Brown hareketi, su moleküllerinin sürekli olarak minik polen tanelerine çarpmasından olur. Gözle görülemeyen su molekülleri gelişigüzel hareket eder ve birbirleriyle çarpışırlar. Bu sırada polenlerle de çarpışıp onları hareket ettirirler. Polen tanesi su moleküllerinden yüzlerce kat büyük olsa da gelişigüzel yönlerde ilerleyen birçok molekül aynı anda kendisine çarptığı için genellikle bir kuvvet dengesizliği oluşur ve polen bir yöne doğru hareket eder. Bu sürekli olduğundan, polen sendeleyerek ilerleyen bir sarhoşunkine benzeyen zikzaklı bir yol izler ve su moleküllerinin çarpması rastgele olduğundan, polenin izleyeceği yol önceden tahmin edilemez. Dolayısıyla polen her an yön değiştirebilir.
Brown hareketi sıvı ya da gazlarda asılı bütün küçük parçacıklar için geçerlidir. Hatta -büyüteçle incelendiğinde- havada dans edercesine süzülen dumanı oluşturan büyükçe parçacıkların bile etkilendiği görülebilir. Parçacıkların aldığı minik darbelerin şiddeti, moleküllerin momentumuna bağlıdır. Yani sıvı ya da gazı oluşturan moleküller ağırsa veya akışkan sıcak olduğu için hızlı hareket ediyorlarsa, yarattıkları sarsıntılar da daha şiddetli olur.
19. yüzyılın sonlarında Brown hareketinin altında yatan matematiğin ortaya çıkarılmasına çalışıldı. Ama onu fizikçilerin dikkatine sunan kişi 1905’te yazdığı bir makaleyle Einstein oldu. 1905 yılı aynı zamanda Einstein’ın kendi geliştirdiği görelilik kuramı ve kendisine Nobel Ödülü kazandıran fotoelektrik etki üzerine iki makale daha yazdığı yıldı. Einstein, Brown’ın gözlemlediği hareketleri başarılı bir şekilde açıklamak için moleküllerin çarpışmasına dayanan ısı kuramından yararlanmıştı. Brown hareketinin akışkanlarda moleküllerin varlığına yönelik kanıt oluşturduğunu gören fizikçiler atom kuramını kabul etmek zorunda kaldı, çünkü atom kuramı 20. yüzyılın başlarında bile hâlâ sorgulanıyordu.
Difüzyon
Brown hareketi parçacıkların zamanla ciddi mesafeler ilerlemesine neden olabilir. Ama bu ilerleme hiçbir engelle karşılaşılmayan ve dümdüz giden parçalarınki gibi hızlı olmaz. Ne de olsa rastgele çarpışmalar parçacıkları ileri olduğu gibi geri de hareket ettirebilir. Örneğin bir sıvıya bir noktadan bir grup parçacık bırakılırsa, sıvı hiç karıştırılmasa ya da içinde hiçbir akıntı olmasa bile parçacıklar dışa doğru yayılır. Her parçacık kendi yolunda ilerler; bu da bir arada yoğun olarak bulunan parçacıkların dağılarak bir difüzyon veya yayınım bulutu oluşturmasına neden olur. Böylesi bir difüzyon, örneğin atmosferdeki aerosollerde olduğu gibi, kirlenmenin bir kaynaktan yayılışını anlamak açısından önemlidir. Hiç rüzgâr olmasa da havadaki kimyasal maddeler Brown hareketi nedeniyle yayılırlar.

Fraktallar
Fraktallara bir örnek, Brown hareketinin ilerlettiği bir parçacığın izlediği yoldur. Yolun her aşaması herhangi bir büyüklükte ve yönde olabilir ama bu genel bir örüntünün varlığına engel değildir. Bu örüntünün en küçük parçasından en büyük parçasına kadar geçerli olan bir yapısı vardır ki zaten fraktalı fraktal yapan da budur.
Fraktallar 1960’lı ve 1970’li yıllarda Benoit Mandelbrot tarafından “kendine benzer” şekilleri sayı şal yoldan ifade edebilmenin bir yolu olarak tanımlandı. Fraktallar, görünüşü her ölçekte aynı olan desenlerdir. De-senin küçük bir bölümü alınıp büyütüldüğünde, büyük ölçekteki şekilden hiçbir farkı olmadığı görülür. Dolayısıyla yalnızca şekle bakarak ne kadar büyütülmüş olduğuna dair bir şey söylenemez. Bu tür yinelenen ve ölçeksiz desenlere doğada sık rastlanır. Ağaçların dalları, eğrelti otlarının yaprakları, kıyıların kıvrımları veya kar tanelerinin simetrik yapısı hep bu tür desenler oluşturur.
Uzunlukları ve boyutları bakılan ölçeğe bağlı olduğu için ortaya kesirli boyutlar çıkar. Aynı kıyıda yer alan iki kasaba arasındaki uzaklığı ölçtüğünüzde, sözgelimi 30 km çıkabilir. Ama her bir kayayı göz önüne alır ve bir iple onların çevresinden dolaşarak ölçmeye kalkarsanız, yüz kilometrelik bir ipe ihtiyacınız olur. Daha da ileri gidip kıyıdaki her kum tanesinin çevresinden dolaşarak ölçerseniz, yüzlerce kilometre uzunluğunda bir ip gerekebilir. Yani burada mutlak uzunluk, ölçüm yapılan ölçeğe bağlıdır. Ama netlikten uzaklaşıp kabaca bir ölçümle yetinirseniz, 30 kilometreye dönebilirsiniz. Bu bağlamda, fraktal boyutlar şekillerin -örneğin bir bulutun, bir ağacın ya da bir sıradağın- pürüzlülüğünü ölçer. Pek çok fraktal şekil, tıpkı bir kıyı şeridinin ana hatlarında olduğu gibi, rassal adımlarla ilerleyerek üretilebilir. Bu açıdan Brown hareketiyle ilişkilidirler.
Brown hareketinin matematiği
Brown hareketinin matematiği, yani bir rassal hareketler dizisi, bilimin birçok alanında işe yarayacak birtakım fraktal örüntüler üretmek için kullanılabilir. Bilgisayar oyunları için kabaca şekil verilmiş dağlar, ağaçlar ve bulutlar gibi sanal manzaralar yaratılabilir. Çukurları ve tümsekleri modelleyerek robotların engebeli arazide ilerlemesini sağlayan uzamsal harita programlarında kullanılabilirler. Bedenimizde bronşların kalın dallardan incelere doğru dallandığı akciğerler gibi bazı karmaşık bölümlerin yapısını analiz etmek isteyen doktorlar, onlardan tıbbi görüntülemede yararlanabilir.
Brown hareketinin altında yatan fikirler, su taşkınlardan borsa dalgalanmalarına kadar birçok ufak rassal olayın toplam ürünü olan olayların ve risklerin tahmin edilmesinde de yararlıdır. Borsa, tıpkı Brown hareketiyle ilerleyen bir dizi molekül gibi, rastgele değişen hisselerden oluşan bir portföy olarak düşünülebilir. Brown hareketi üretim ya da karar verme gibi daha başka toplumsal süreçlerin modellenmesinde de kullanılabilir. Brown hareketindeki rastgele ilerleyişin geçmişte birçok alanda büyük etkisi olmuştur ve güzel bir bardak sıcak çayın içindeki minik çay yapraklarının dansından başka daha pek çok yerde karşımıza çıkar.