Çemberde Benzerlik Formülleri, Özellikleri, Çözümlü Örnek Sorular

Çemberde Benzerlik nedir? Çemberde benzerlik özellikleri ve formülleri nelerdir? Çemberde benzerlik konu anlatımı, örnek soru çözümleri.

Çemberde Benzerlik

Bütün çemberler benzerdir. Merkez açıları eşit olan bütün çember yaylarıda benzerdir.

Çevreleri oranı benzerlik oranına eşittir. Benzerlik oranı $\displaystyle \frac{r}{{{r}_{1}}}$ dir.

Örnek

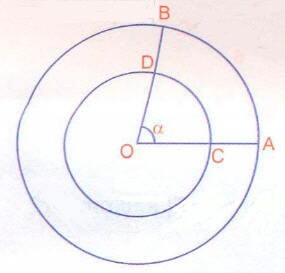
|OD| = 2.|BD|
|DC| = 12 cm
O noktası her iki çemberin merkezidir. Buna göre, |AB| kaç cm dir?

Çözüm

|BD| = k olursa |OD| = 2k ve
|OB| = 3k olur. buradan yarıçapları oranı

$\displaystyle \frac{\left| OD \right|}{\left| OB \right|}=\fr\right|ac{2k}{3k}$
$\displaystyle \frac{2}{3}=\frac{\left| \overset\frown{DC} \right|}{\left| \overset\frown{AB} }$
$\displaystyle \frac{2}{3}=\frac{12}{\left| \overset\frown{AB} \right|}$ buradan $\displaystyle \left| \overset\frown{AB} \right|=18$ cm. dir.

Örnek

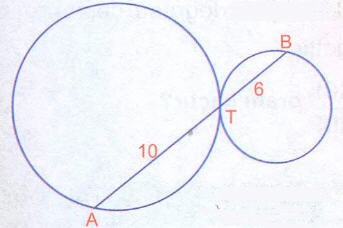
|BT| = 6 cm
|AT| = 10 cm
|BT| = 9 cm

Yukarıdaki şekilde verilen çemberler birbirlerine T noktasında dıştan teğettir.

Buna göre, AT yayının uzunluğu kaç cm dir?

Çözüm

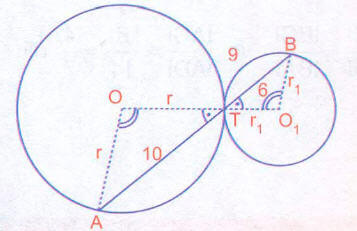
Merkezler ve teğet nokta doğrusaldır. O halde; $\displaystyle \text{AOT }\!\!\tilde{\ }\!\!\text{ B}{{\text{O}}_{1}}T$ olur.

$\displaystyle \frac{{{r}_{1}}}{r}=\frac{6}{10}$ ve BT yayı ile AT yayını gören r 10

merkez açılarıda eşit olduğuna göre, bu yaylarda benzerdir.

$\displaystyle \frac{\left| \overset\frown{BT} \right|}{\left| \overset\frown{AT} \right|}=\frac{{{r}_{1}}}{r}$ buradan
$\displaystyle \frac{9}{\left| \overset\frown{AT} \right|}=\frac{6}{10}$ ve $\displaystyle \left| \overset\frown{AT} \right|=15cm$

Örnek

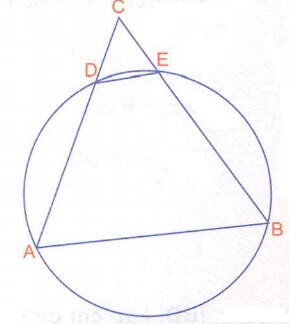
ABC bir üçgen |EC| = 6 cm
|AC| = 15 cm
|DE| = 5 cm
Yukarıdaki verilere göre, |AB| kaç cm dir?

Çözüm

ABED bir kirişler dörtgeni olduğu için karşılıklı açıları toplamı 180° dir. O halde

m(CAB) = m(CED) ve
m(ABC) = m(EDC) olacağından
CDE ~ CBA benzerliği görülmelidir.

$\displaystyle \frac{\left| CD \right|}{\left| CB \right|}=\frac{\left| CE \right|}{\left| CA \right|}=\frac{\left| DE \right|}{\left| BA \right|}$ buradan

$\displaystyle \frac{6}{15}=\frac{5}{\left| AB \right|}\Rightarrow \left| AB \right|=12,5cm$

$\displaystyle \left| AB \right|=\left| AC \right|=x$
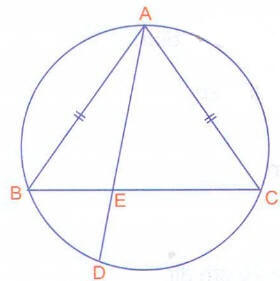
A, E, D doğrusal
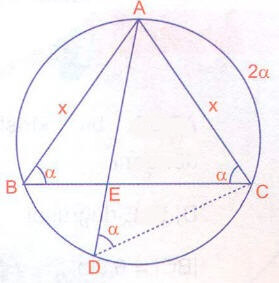
$\displaystyle {{x}^{2}}=\left| AE \right|.\left| AD \right|$

$\displaystyle m\left( \overset\frown{ABC} \right)=m\left( \overset\frown{ACB} \right)=m\left( \overset\frown{ADC} \right)=\alpha$

$\displaystyle ACE\sim ADC$ benzerliğinden

$\displaystyle \frac{\left| AC \right|}{\left| AD \right|}=\frac{\left| AE \right|}{\left| AC \right|}$ buradan
$\displaystyle {{x}^{2}}=\left| AD \right|.\left| AE \right|$
formülü oluşur.

|AB| = |AC|= x
A, D, E ve
B, C, E doğrusal
$\displaystyle {{x}^{2}}=\left| AD \right|.\left| AE \right|$

$\displaystyle m\left( \overset\frown{ABC} \right)=m\left( \overset\frown{ACB} \right)=\alpha$ olsun.
$\displaystyle m\left( \overset\frown{ADC} \right)=180-\alpha$ (kirişler dörtgeni)
$\displaystyle m\left( \overset\frown{ACE} \right)=180-\alpha$ olur.
$\displaystyle ADC\sim ACE$ benzerliğinden
$\displaystyle \frac{\left| AD \right|}{\left| AC \right|}=\frac{\left| AC \right|}{\left| AE \right|}$ buradan
$\displaystyle {{x}^{2}}=\left| AD \right|.\left| AE \right|$

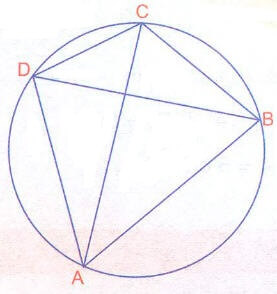
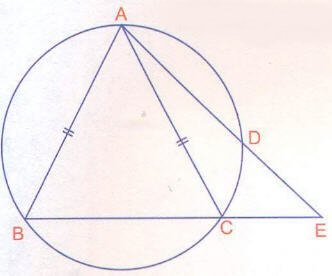
ABCD bir kirişler dörtgeni [AC] , [BD] köşegen ise

|AC| . |BD| = |AB| . |DC] + |AD| . |BC|

Köşegenlerin çarpımı, karşılıklı kenarların çarpımlarının toplamına eşittir.

$\displaystyle m\left( \overset\frown{ACD} \right)=m\left( \overset\frown{BCE} \right)=\alpha$ olacak şekilde [CE] çizilirse

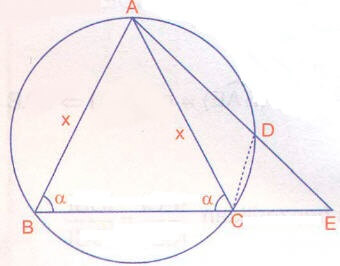
1. ACD ~ BCE (Açı Açı benzerliği)

$\displaystyle \frac{\left| AC \right|}{\left| BC \right|}=\frac{\left| AD \right|}{\left| BE \right|}$ ve
$\displaystyle \left| BC \right|.\left| AD \right|=\left| AC \right|.\left| BE \right|$

2. ABC ~ DEC (Açı Açı benzerliği)

$\displaystyle \frac{\left| AB \right|}{\left| DE \right|}=\frac{\left| AC \right|}{\left| DC \right|}$ ve
$\displaystyle \left| AB \right|.\left| DC \right|=\left| DE \right|.\left| AC \right|$

1. $\displaystyle \left| BC \right|.\left| AD \right|=\left| AC \right|.\left| BE \right|$
2. $\displaystyle \left| AB \right|.\left| DC \right|=\left| DE \right|.\left| AC \right|$

Alt alta toplama yapılırsa