Dik dairesel koni nedir, özellikleri nelerdir? Dik dairesel koninin açılımı, örnek soru ve cevapları, konu anlatımı.
Dik Dairesel Koni
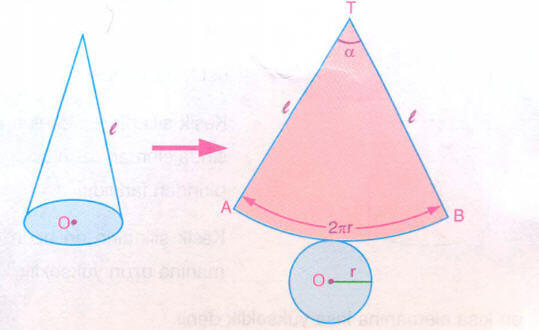
Dik dairesel koninin açınımı, tabanını oluşturan bir daire ile yanal yüzünü oluşturan bir daire diliminden oluşur.
AB yayının uzunluğu, hem koninin taban çevresine hem de yarıçaplı, α merkez açılı çember diliminin uzunluğuna eşit olduğundan,
olur.
Buna göre, bir dik koninin taban yarıçapı ile ana doğrusu arasında bağıntısı yazılabilir.
Buradaki α değeri, koninin yanal yüzünün açınımı olan daire diliminin merkez açısının ölçüsüdür.
Örnek
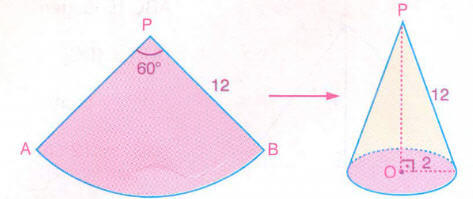
Yarıçap uzunluğu 12 cm ve merkez açısının ölçüsü 60° olan bir daire dilimi kıvrılarak, dik koni elde ediliyor.
Buna göre, koninin taban yarıçapını bulalım.
Çözüm:
Örnek:
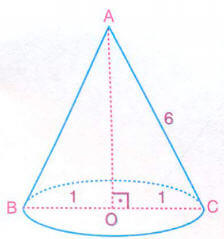
A dik koninin tepesi [BC] koni tabanının çapı |BO| = |OC| = 1 cm
|AC| = 6 cm
Şekilde, B noktasından çıkan bir karınca en kısa yoldan [AC] kenarına ulaştığında A noktasına olan uzaklığının kaç cm olduğunu bulalım.
Çözüm
Koninin yan yüzünü oluşturan daire diliminin merkez açısı a olsun.
Yukarıdaki şekilde, = 6 cm ve r = 1 cm olduğundan,
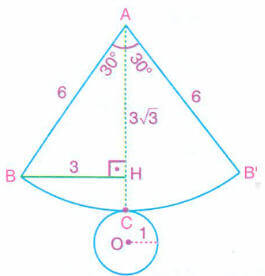
Buna göre, koninin yan yüzünün açınımı
|AB| = |AB’| = 6 cm olacak şekilde bir daire dilimi olur. Şekilde,
A noktasından [AC] ye en kısa yol, [BH] doğru parçasıdır.
ABH (30° – 60° – 90°) dik üçgeninde |AB| = 6 cm olduğundan,
|BH| = 3 cm ve |AH| = cm olur.
Buna göre, karınca [AC] kenarına ulaşınca yani H noktasına
geldiğinde A ya uzaklığı cm bulunur.