Dönen Cisimlerin Kinetik Enerjisi ve Eylemsizlik Momenti

Dönen cisimlerin kinetik enerjisi nasıl hesaplanır? Eylemsiz momenti nedir, özellikleri, dönen cisimlerde formüller, örnekli konu anlatımı.

Dönen Cisimlerin Kinetik Enerjisi ve Eylemsizlik Momenti

donen-cisim Buz üzerinde-gösteri yapan bir sporcu, kollarını yana açmış olarak ayakta dönerken, kollarını ansızın kapatırsa daha hızlı dönmeye başlar. Dönme hareketlerinde buna benzer ilginç olaylar gözlenir. Sporcu, kollarını kapatmakla hızı arttırıcı bir kuvvet mı yaratmıştır. Hayır! Peki nasıl oluyor da dönerken kollarını kapatınca daha hızlı dönüyor? Bu sorunun yanıtı, dönme hareketlerindeki kinetik enerjinin neye bağlı olduğu gerçeğinde saklıdır. İşte bu amaçla dönen bir cismin kinetik enerjinin nelere bağlı olduğunu saptamaya çalışacağız.

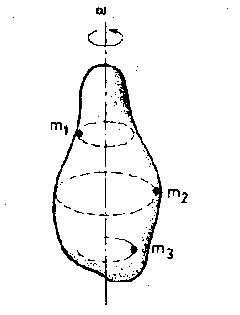
Düşey bir eksen çevresinde sabit bir ω açısal hızı ile dönen katı bir cismi gözönüne alalım. Bu cismin, mx, m2, m, , … gibi noktasal kütlelerden oluştuğunu düşünelim. Cismin tüm M kütlesi, bu noktasal kütlelerin toplamıdır.

$\displaystyle M={{m}_{1}}+{{m}_{2}}+{{m}_{3}}+....+{{m}_{n}}$

Bu noktasal kütleler, eksen çevresinde aynı açısal hızla dönerler. Fakat çizgisel hızları, eksene uzaklıklarına göre değişir. Çizgisel hızlar, v = rω bağıntısına göre,

$\displaystyle {{v}_{1}}={{r}_{1}}\omega ,{{v}_{2}}={{r}_{2}}\omega ,{{v}_{3}}={{r}_{3}}\omega ,.....,{{v}_{n}}={{r}_{n}}\omega$

dır. Cismin tüm kinetik enerjisi, bu noktasal parçacıkların kinetik enerjilerinin toplamı olacağından,

$\displaystyle KE=\frac{1}{2}{{m}_{1}}v_{_{1}}^{2}+\frac{1}{2}{{m}_{2}}v_{2}^{2}+\frac{1}{2}{{m}_{3}}v_{3}^{2}+...+\frac{1}{2}{{m}_{n}}v_{n}^{2}$

$\displaystyle KE=\frac{1}{2}{{m}_{1}}{{\left( {{r}_{1}}\omega \right)}^{2}}+\frac{1}{2}{{m}_{2}}{{\left( {{r}_{2}}\omega \right)}^{2}}+\frac{1}{2}{{m}_{3}}{{\left( {{r}_{3}}\omega \right)}^{2}}+...+\frac{1}{2}{{m}_{n}}{{\left( {{r}_{n}}\omega \right)}^{2}}$

$\displaystyle KE=\frac{1}{2}\left( {{m}_{1}}{{r}_{1}}^{2}+{{m}_{2}}{{r}_{2}}^{2}+{{m}_{3}}{{r}_{3}}^{2}+...+{{m}_{n}}{{r}_{n}}^{2} \right){{\omega }^{2}}$

elde edilir. Parantez içindeki toplam, benzer terimlerden oluşmaktadır. Her terim “Kütle x yarıçap²” dir. Bu toplam, kütlelerin eksen çevresinde nasıl dağılmış olduğuna bağlıdır. Aynı kütleye sahip iki cisim aynı açısal hızla dönerken, hangisinin mr² ler toplamı büyükse onun kinetik enerjisi daha büyük olur. Öteleme hareketlerinde de aynı hıza sahip iki cisimden kütlesi büyük olanın kinetik enerjisi büyük oluyordu. O halde dönme hareketlerinde kütlenin yerini mr² ler toplamı almaktadır. Aynı bir cismin bu mr² ler toplamına o cismin eylemsizlik momenti denir ve I ile gösterilir.

$\displaystyle I={{m}_{1}}r_{1}^{2}+{{m}_{2}}r_{2}^{2}+...+{{m}_{n}}r_{n}^{2}$

Eylemsizlik momenti, cismin geometrik şekline bağlı bir niceliktir. Örneğin kütleleri eşit bir silindir ile bir kürenin eylemsizlik momentleri farklı olduğu gibi, eşit kütleli dolu bir silindirle içi boş silindirin eylemsizlik momentleri de farklıdır.

Kısacası, eylemsizlik momenti kütlenin dönme ekseni çevresinde dağılım biçimine bağlıdır. Aynı bir cismin eylemsizlik momenti, farklı dönme eksenlerine göre de farklı olur.

O halde dönme kinetik enerjisi,
$\displaystyle KE=\frac{1}{2}I{{\omega }^{2}}$

dir. Eylemsizlik momentinin birimi kg.m² dir.

Eylemsizlik momentinin özelikleri :

1. öteleme hareketlerindeki kütlenin yerini, dönme hareketlerinde eylemsizlik momenti alır.
2. Eylemsizlik momenti cismin geometrik şekline ve dönme ekseninin yerine bağlıdır.
3. Eylemsizlik momenti büyük cisimlere dönme hızı vermek daha zordur. Tersine eylemsizlik momenti büyük cisimler belli bir hızdan itibaren daha geç yavaşlarlar.

Yuvarlanan bir cismin hem öteleme hem de dönme kinetik enerjisi vardır. Aynı enerji verilerek harekete geçirilen eşit kütleli iki cisimden biri kayar, öteki yuvarlanırsa; kayan cisim daha çok hız kazanır.