Düzgün yavaşlayan doğrusal hareket nedir, düzgün yavaşlayan doğrusal hareket ivme, hız ve konum denklemleri nelerdir? Düzgün yavaşlayan doğrusal hareket bağıntıları
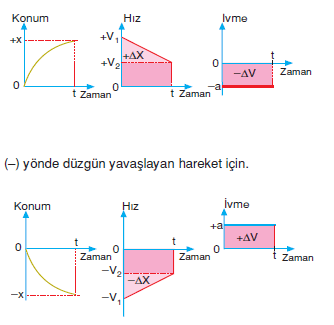
Düzgün Yavaşlayan Doğrusal Hareket
Aşağıdaki çizelgede, düzgün yavaşlayan bir cismin, çeşitli anlardaki hız değerleri verilmiştir.
| Zaman (s) | 0 | 5 | 10 | 15 | 20 | 25 |
| Hız (m/s) | 12 | 10 | 8 | 6 | 4 | 2 |
Çizelgeye göre hızın değerleri her 5 saniyede bir 2 m/s azalmaktadır. Yani ivme sabittir. Üstelik ivme,
dir.
Negatif ivmenin yavaşlama hareketini anlattığını önceki paragraflardan biliyoruz* Art arda gelen anlardaki hız değerleri bu çizelgedeki gibi olan bir hareket düzgün yavaşlayan harekettir. Öyleyse, düzgün yavaşlayan hareketin tanımını şöyle yapabiliriz.
Bir doğru üzerinde, hızı, eşit zaman aralıklarında eşit azalışlar gösteren harekete düzgün yavaşlayan doğrusal hareket denir.
Düzgün Yavaşlayan Doğrusal Hareket Denklemleri
1. İvme denklemi :
Bundan önceki harekette olduğu gibi ivme sabittir. Hareket yavaşlayan olduğu için de ivmenin değeri negatiftir.
= Sabit (negatif)
İvmenin negatifliği, harekete ters yönde olduğunu da anlatır. Bu harekette de ardışık hız değerleri bir aritmetik dizi oluşturduğundan ortalama hız, ilk ve son hızların aritmetik ortalamasıdır.
2. Hız denklemi :
Bu hareketin hız denklemi de, bundan önceki harekette izlediğimiz yoldan çıkarılır. Aynı işlemleri yinelemenin bir yararı olmayacağını düşünerek doğrudan doğruya sonucu yazıyoruz : Hız denklemi
biçimindedir.
3. Konum denklemi :
İlk hız ve ivme belli olduğunda t saniye sonundaki konum,
ile hesaplanır.