Eğik atış hareketi nedir? Eğik Atış Hareketinin bileşenleri, neye bağlıdır, nasıl hesaplanır, grafikleri, nasıl olur, özellikleri açıklanması.

Kaynak: pixabay.com
EĞİK ATIŞ HAREKETİ
Yerçekimi alanında, yatay ya da düşeyle bir açı yapacak biçimde, vo ilk hızıyla atılan cisimlerin yaptığı bileşik harekete eğik atış hareketi denir.
Eğik atış hareketi, bir cismi bir açıyla yukarı doğru fırlattıktan sonra, yatay ve dikey yönlerde ayrı ayrı hareket ettiği bir harekettir. Bu hareket, çeşitli spor etkinliklerinde (basketbol, voleybol, futbol, beyzbol vb.) ve birçok endüstriyel uygulamada önemli bir rol oynamaktadır.
Nelere Bağlıdır?
Eğik atış hareketi, aşağıdaki faktörlere bağlıdır:
- Fırlatılan cismin hızı: Fırlatılan cismin hızı, cismin dikey yüksekliği ve yatay mesafesi üzerindeki etkisini belirleyecektir. Daha yüksek bir hız, cismin daha yüksek bir yere çıkmasına ve daha uzağa gitmesine neden olacaktır.
- Atış açısı: Atış açısı, cismin dikey yüksekliği ve yatay mesafesi üzerindeki etkisini belirleyecektir. Daha yüksek bir açı, cismin daha yüksek bir yere çıkmasına ve daha kısa bir yatay mesafede gitmesine neden olacaktır.
- Cismin kütlesi: Cismin kütlesi, cismin hızı ve dikey yüksekliği üzerinde etkili olacaktır. Daha ağır bir cisim, aynı hız ve açı ile fırlatıldığında daha düşük bir yüksekliğe çıkacaktır.
- Çekim ivmesi: Yer’in kütleçekim ivmesi, cismin dikey yüksekliği üzerinde doğrudan etkilidir. Daha yüksek bir çekim ivmesi, aynı hız ve açı ile fırlatılan bir cismin daha yüksek bir yere çıkmasına ve daha kısa bir yatay mesafede gitmesine neden olacaktır.
Yukarıdaki faktörler, eğik atış hareketinin çeşitli özelliklerini belirleyen ve hareketin matematiksel olarak modellenmesine izin veren bileşenlerdir.
EĞİK ATIŞ HAREKETİN BİLEŞENLERİ
Eğik atış hareketi bileşenleri şunlardır:
- İlk hız bileşenleri: Eğik atış hareketi, ilk hız bileşenleri olan yatay ve dikey bileşenleri içerir. İlk hızın yatay bileşeni, cismin yatayda hareket ettiği hızı ifade ederken, dikey bileşeni, cismin dikeyde hareket ettiği hızı ifade eder.
- Atış açısı: Atış açısı, cismin yatay ve dikey hız bileşenlerinin oranını belirler. Bu açı, cismin dikey yüksekliğini ve yatay mesafesini etkiler.
- Dikey hareket bileşenleri: Eğik atış hareketi, dikey hareket bileşenlerini içerir. Bu bileşenler, cismin dikeyde hareket ettiği hızı ve yüksekliği ifade eder.
- Yatay hareket bileşenleri: Eğik atış hareketi, yatay hareket bileşenlerini içerir. Bu bileşenler, cismin yatayda hareket ettiği hızı ve mesafeyi ifade eder.
Bu bileşenler, eğik atış hareketinin matematiksel olarak modellenmesine olanak tanır ve çeşitli hareket özelliklerini belirleyen denklemleri ifade eder. Örneğin, yatay hareket bileşenleri sabit kalırken, dikey hareket bileşenleri yerçekimi ivmesi tarafından etkilenecektir. Bu nedenle, eğik atış hareketinin denklemleri, çeşitli bileşenleri içerecek şekilde yazılabilir ve hareketin özellikleri, bileşenlerin etkileşimine göre analiz edilebilir.
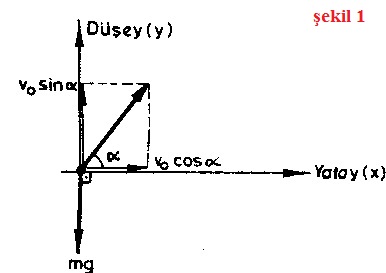
Cismin vo atılış hızını, Şekil 1 deki gibi, düşey vo Sinα ve yatay vo Cosα bileşenlerine ayıralım. Yerçekimi kuvveti mg, hızın yatay bileşenine dik olduğundan bunu değiştirmez. Düşey bileşen ise mg ye ters yönde olduğundan önce azalır, bir an sıfır olur, sonra ters yönde artar. Bu nedenle cisim yatayda sabit hızla (vo Cos α ile) giderken bir yandan da vo Sinα etkisiyle önce biraz yükselir, sonra geri iner. Bu iki etkinin sonucunda da yörünge Şekil 2’deki gibi olur. O halde hareketin bileşenleri,
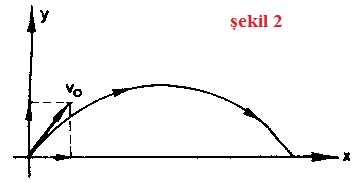
I. Yatayda vo Cos α hızıyla düzgün doğrusal, yani sabit hızlı hareket,
II. Düşeyde önce vo Sinα hızıyla düşey atış, sonra da serbest düşme hareketi olarak özetlenebilir.
Nasıl Hesaplanır?
Eğik atış hareketinin çeşitli özelliklerini hesaplamak için, aşağıdaki adımları takip edebilirsiniz:
- İlk hız bileşenlerini hesaplayın: İlk hızın yatay bileşeni, cismin yatayda hareket ettiği hızı ifade ederken, dikey bileşeni, cismin dikeyde hareket ettiği hızı ifade eder. İlk hız bileşenlerini, atış açısı ve toplam hızdan yararlanarak hesaplayabilirsiniz.
- Dikey hareket bileşenlerini hesaplayın: Dikey hareket bileşenleri, cismin dikeyde hareket ettiği hızı ve yüksekliği ifade eder. Yerçekimi ivmesi, dikey hareket bileşenlerinin değerlerini etkileyecektir. Dikey bileşenlerin değerleri, zamanın karesiyle orantılı olarak azalacaktır. İlk dikey hız bileşeni, aşağı doğru negatif bir değerdir.
- Yatay hareket bileşenlerini hesaplayın: Yatay hareket bileşenleri, cismin yatayda hareket ettiği hızı ve mesafeyi ifade eder. Yatay bileşenler sabit kalır ve yerçekimi tarafından etkilenmez.
- Dikey yüksekliği ve mesafeyi hesaplayın: Eğik atış hareketi sırasında, cismin yatay ve dikey bileşenleri ayrı ayrı hesaplanabilir. Bu bileşenlerin birleşimi, cismin konumunu ve hareketini belirleyecektir. Dikey yükseklik, dikey hareket bileşenlerinin zamanın karesiyle çarpımından hesaplanabilirken, mesafe yatay hareket bileşeninin zamanla çarpımından hesaplanabilir.
Eğik atış hareketinin çeşitli özelliklerini hesaplamak için, yukarıdaki adımları takip ederek, uygun denklemleri kullanabilirsiniz. Bu hesaplamalar, hareketin matematiksel olarak modellenmesine ve analiz edilmesine olanak tanır.
EĞİK ATIŞ HAREKETİN ÖZELİKLERİ
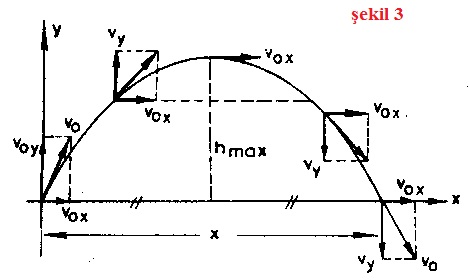
- I. Kütleye bağlı değildir.
- II. Hızın yatay bileşeni hareket, süresince değişmez.
- III. Hızın düşey bileşeni, vo Sinα dan itibaren önce düzgün azalır, tepede sıfır olur, sonra düzgün olarak yine vo Sinα değerine ulaşır.
- IV. Yörüngenin tepe noktasında düşey hız sıfırdır, yalnızca vo Cosα hızı vardır.
- V. Cismin yörünge tepesine çıkış süresi, iniş süresine eşittir.
- VI. Cisim yörünge üzerinde aynı düzeydeki noktalardan eşit değerde hızlarla geçer. (Şekil 3)
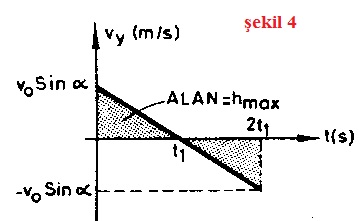
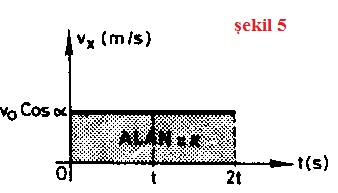
Eğik atışta cismin hızının düşey bileşeninin zamanla değişimi Şekil 4 de, yatay hızının zamanla değişimi ise Şekil 5 deki gibidir. Düşey bileşene ait hız-zaman grafiğinin altındaki alanlardan biri cismin çıkabildiği maksimum yüksekliği verir. Yatay bileşene ait hız-zaman grafiğinin altındaki alan ise alınan yatay yolu verir.
Cisim yatay x yolunu vo Cos α sabit hızıyla gider. Maksimum yüksekliği ise yörüngenin tepe noktasından sonra serbest düşmeyle iner.
Kaynak 2
Eğik Atış Hareketi
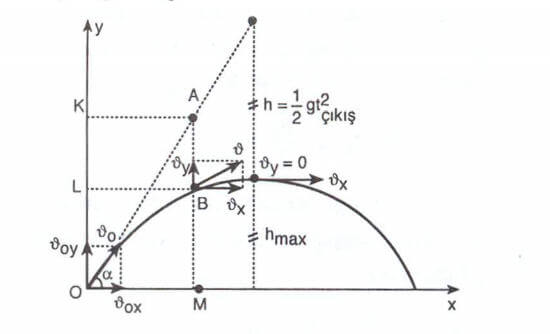
Bir cisim ilk hızı ile yatayla a açısı yapacak şekilde O noktasından atılırsa cisim sahip olduğu
hızı ile t saniye
kadar yol alır. Ayrıca yerçekiminin etkisiyle de
aşağı düşer. B noktasının koordinatları
dir.
Eğik atış hareketini; cismin hızı ile düşey doğrultuda yapılan yukarı doğru düşey atış hareketi, diğeri
sabit hızı ile yatay doğrultuda yapılan öteleme hareketinin bileşkesi gibi düşünebiliriz.
Cismin t saniye sonundaki hızının bileşenleri
olup, cismin hızı
dir.
Cismin eriştiği maksimum yükseklik;
Cismin uçuş süresince yatay doğrultuda aldığı yola menzil denir.
bağıntısından hesaplanır.
1 Yorum
Bilgiler güzel paylaştım