Geometride temel bilgiler ve terimler ile ilgili bilgiler. Nokta, düzlem, eğri, çizgi, derinlik, genişlik nedir?
Hayatın hesaba dayanan işlerin de aritmetik kadar geometrinin de büyük önemi vardır. Alışveriş ederken, alacağımız malın miktarını, ne kadar para vereceğimizi hesaplamamız nasıl gerekirse, bir şeyin biçimini anlatabilmek için de bir geometri bilgimiz olması gerekir.
Kardeşinize kağıttan kayık nasıl yapılacağını anlatmak, öğretmek istiyorsunuz diyelim. Kağıdı dört köşe (kare) biçiminde kesmesini söylersiniz. Uçurtma yapacaksanız, kağıtları üç köşe (üçgen) biçiminde kesilecektir. Uçurtmayı yaparken, 6 tane üçgeni uçlarından bir merkezde toplayıp yan yana getirince ortaya bir altı köşe (altıgen) çıkar.
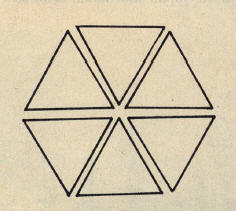
Yalnız, dikkat edin: Bütün bunları yaparken ilk önce neye başvuruyorsunuz? Cetvelle kaleme, değil mi? Çünkü, kağıtları doğru kesebilmek için önce üzerine çizgi çizmek gerekir. Demek oluyor ki bir biçimi meydana getirebilmek için ilk gerekli şey çizgidir.
Şimdi, cetvelimizi alıp kağıdın üzerine cetvel boyunca bir çizgi çizelim. Cetvelin uzun kenarı düzgün olduğu için çizdiğimiz çizgi de düzgün olacaktır, işte bu gibi çizgilerin hepsine birden düz çizgi, ya da doğru denir.
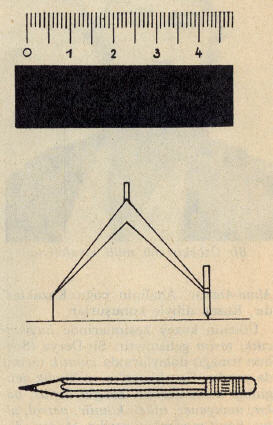
Doğrunun iki ucu sınırsızdır, istediğimiz kadar uzatabiliriz. Doğrunun bir yanını sınırlarsak yarım doğru elde ederiz. iki yanını da sınırlarsak ortaya çıkan şekle doğru parçası denir. Demek ki bir doğrunun iki noktası arasında kalan parçası doğru parçasıdır.
Bir de doğru olmayan çizgiler vardır. Bir maden parayı defterimizin üzerine koyup kalemimizi paranın çevresinde biraz dolaştırırsak, gene bir çizgi elde ederiz ama, bu bir doğru değildir, işte bu gibi çizgilere de eğri çizgi deriz.
Para ile bir çember parçası elde etmiş oluruz. Demek çember parçası eğri çizgidir. Ne var ki bütün eğri çizgiler çember parçası değildir. Kalemi şöyle elimizle bir dolaştırıp köşesiz bir çizgi çizersek ortaya eğri çizgi çıkar.
Bir de kırık çizgi vardır. Çeşitli doğru paçalarını rastgele birbirine eklersek kırık çizgi elde ederiz. Doğru parçalarını aynı doğrultuda arka arkaya sıralarsak kırık çizgi değil, daha uzun bir doğru parçası çizmiş oluruz.
NOKTA, BOYUT, YÜZEY
İki doğrunun kesişmesiyle elde edilen geometri şekline nokta denir. Nokta büyük harfle gösterilir.
Geometride noktanın hiçbir boyut’u yoktur. Yani noktanın eni, boyu, yüksekliği sıfır kabul edilir. Bir noktanın kesintisiz yer değiştirmesiyle çizgi elde edilir.
Demek oluyor ki çizginin tek boyutu vardır: uzunluğu.
Çizgilerin çeşitli doğrultularda hareket etmesiyle yüzey’ler ortaya çıkar. Masa, cam gibi düzgün yüzeylere ise düzlem adı verilir. Yüzeylerin hareketi ise bize cisim’leri verir. Buradan çıkan sonuca göre:
•Düzlemlerin iki boyutu vardır: eni, boyu.
•Hacimlerin ise üç boyutu vardır; en, boy, yükseklik (ya da genişlik, derinlik, yükseklik).
Bir dolap örneğinde bunu kolayca görürüz. Dolap dik dörtgenler prizması biçiminde bir cisimdir. Bir derinliği, bir genişliği, bir de yüksekliği vardır.
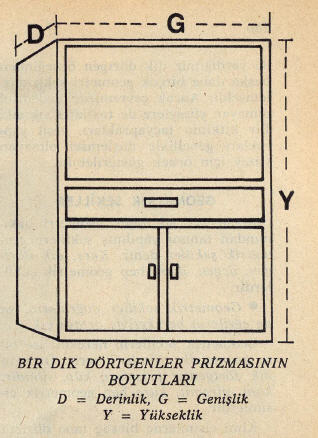
Geometri çizgileri, yüzeyleri, cisimleri inceleyen bir bilim dalıdır. Aynı özelliği taşıyan yüzeylere birer ad verilir: Kibrit kutusunu defterimizin üzerine koyup çizerek elde ettiğimiz şeklin adı dikdörtgen’dir. Buna benzeyen bütün şekillere de «dikdörtgen» deriz. Bir dik dörtgenin özellikleri bütün dik dörtgenlerde bulunur.
Defterimizin sayfası bir düzlem olduğuna göre, çizdiğimiz dik dörtgen bu düzlemi iki parçaya ayırır: Birinci parça, dik dörtgenin içinde kalan düzlem parçasıdır, öteki de dik dörtgenin dışında kalan düzlem parçası. Bunun gibi, bütün kapalı şekiller üzerine çizildikleri düzlemi iki parçaya ayırırlar.
Buradan şu sonucu çıkarabiliriz. Kimi geometri şekilleri düzlemsel’dir; yani, bir düzlem üzerine çizilirler. Yukarıda verdiğimiz dik dörtgen örneğinden başka daha birçok geometri şekli düzlemseldir. Ancak, çevremizde düzlemsel olmayan yüzeylere de rastlarız sık sık. Bir bitkinin taç yaprakları, yeşil yaprakları genellikle düzlemsel olmayan yüzey için örnek gösterilebilir.