Harmonik ortalama nedir, ne amaçla ve nasıl hesaplanır? Harmonik ortalamanın formülü nasıldır? Harmonik ortalama örnekleri hesaplaması.
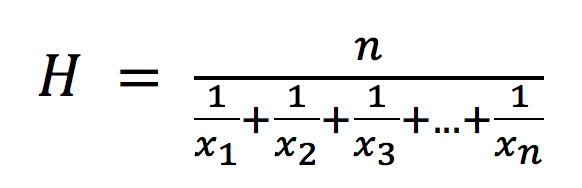
Harmonik Ortalama Nedir?
Harmonik ortalama bir nümerik ortalama türüdür. Harmonik ortalama, bir sayı kümesinin ortalamasını hesaplamak için kullanılır. Eleman sayısının ortalaması alınır ve elemanların karşılıklarının toplamına bölünür.
Gözlem sayısının, gözlemin karşılıklı toplamına bölünmesiyle hesaplanır.
1,4 ve 4’ün harmonik ortalaması:
a ve b gibi iki sayının harmonik ortalaması;
dir.
ÖRNEK;
5 ve 8 sayılarının harmonik ortalamasını bulalım.
Harmonik Ortalamanın Temelleri
Harmonik ortalama, ortak paydalar hakkında endişelenmeden, kesirler arasında çarpma veya bölme ilişkileri bulmaya yardımcı olur. Harmonik araçlar genellikle oranlar gibi şeylerin ortalamasında kullanılır (örneğin, birkaç yolculuk süresi verilen ortalama seyahat hızı).
Ağırlıklı harmonik ortalama, her veri noktasına eşit ağırlık verdiği için finansta fiyat kazanç oranı gibi ortalama katlara kullanılır. Bu oranların ortalamasını almak için ağırlıklı bir aritmetik ortalama kullanılması, yüksek veri noktalarına düşük veri noktalarından daha fazla ağırlık verecektir, çünkü kazançlar eşitlenirken fiyat kazanç oranları fiyat normalleştirilmez.
Harmonik ortalama, ağırlıkların 1’e eşit olduğu ağırlıklı harmonik ortalamadır. W1, w2, w3 ilgili ağırlıkları olan x1, x2, x3’ün ağırlıklı harmonik ortalaması şu şekilde verilir:
Harmonik Ortalama ve Aritmetik Ortalama ve Geometrik Ortalama
Ortalamaları hesaplamanın diğer yolları arasında basit aritmetik ortalama ve geometrik ortalama bulunmaktadır. Aritmetik ortalama, bir sayı dizisinin toplamının, bu sayı dizisinin sayısına bölünmesiyle elde edilir. Test puanlarının sınıf (aritmetik) ortalamasını bulmanız istendiyse, öğrencilerin tüm test puanlarını toplamanız ve daha sonra bu toplamı öğrenci sayısına bölebilirsiniz. Örneğin, beş öğrenci sınava girdiyse ve puanları% 60,% 70,% 80,% 90 ve% 100 olsaydı, aritmetik sınıf ortalaması% 80 olurdu.
Geometrik ortalama, bir yatırımın veya portföyün performans sonuçlarını belirlemek için yaygın olarak kullanılan bir dizi ürünün ortalamasıdır. Teknik olarak “n sayısının n’inci kök ürünü” olarak tanımlanır. Geometrik ortalama, değerlerden elde edilen yüzdelerle çalışırken standart aritmetik ortalama değerlerin kendileriyle çalışırken kullanılmalıdır.
Harmonik ortalama en iyi oranlar veya katlar gibi kesirler için kullanılır.