Hidrojen Atomunun Spektrumu

Hidrojen atomunun spektrumu nedir, nasıldır? Atom fiziği hidrojen atomunun spektrumu konu anlatımı, açıklaması.

Hidrojen Atomunun Spektrumu

hidrojen-atom-spektrumu Uyarılmış bir atomda elektron, yüksek enerjili bir yörüngeden düşük enerjili bir yörüngeye geçerken yayılan fotonun frekansı,

$\displaystyle \upsilon =\frac{{{E}_{\dot{I}}}-{{E}_{s}}}{h}$

dalga boyu ise,

$\displaystyle \lambda =\frac{c}{\upsilon }=\frac{hc}{{{E}_{i}}-{{E}_{s}}}$ dir.

Bir hidrojen atomunda elektron n= 1 seviyesinde bulunuyorsa, atom temel haldedir. O halde,

$\displaystyle {{E}_{n}}=-R\frac{{{Z}^{2}}}{{{n}^{2}}}$

bağıntısında n=l ve Z=1 değerleri yerine konulursa hidrojen atomunun temel haldeki enerjisi bulunmuş olur. (e = 13,6 eV)

$\displaystyle n=1\Rightarrow {{E}_{1}}=-13,6eV$
$\displaystyle n=2\Rightarrow {{E}_{2}}=-3,4eV$
$\displaystyle n=3\Rightarrow {{E}_{3}}=-1,51eV$
$\displaystyle n=4\Rightarrow {{E}_{4}}=-0,85eV$
$\displaystyle n=5\Rightarrow {{E}_{5}}=-0,54eV$
$\displaystyle n=6\Rightarrow {{E}_{6}}=-0,38eV$
.
.
.
$\displaystyle n=\infty \Rightarrow E=0$

Temel halin enerjisi sıfır kabul edilirse, yani +13,6 eV değeri yörünge enerjilerine eklenirse

$\displaystyle {{E}_{1}}=0$
$\displaystyle {{E}_{2}}=10,2eV$
$\displaystyle {{E}_{3}}=12,1eV$
$\displaystyle E=13,6eV$

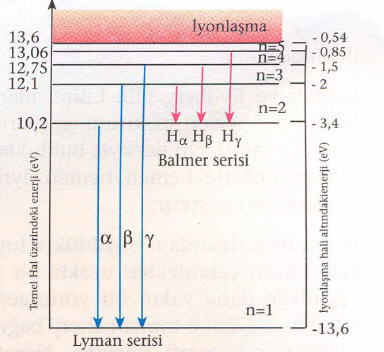
olarak bulunur. Bu enerji seviyeleri ve bunların spektrum çizgilerinden bazıları Şekildeki gibidir. İyonlaşma enerjisinin altındaki enerjilerde elektron protondan sonsuz uzağa gidemez, yani birbirlerine bağlıdırlar. İyonlaşma enerjisinden yüksek enerjilerde ise, elektronla proton birlikte bulunmaz elektron fazladan kinetik enerjiye sahip olacağından protondan ayrı hareket eder. İyonlaşma enerjisinin altındaki enerjilerde elektron belli enerji değerlerlerini (kesikli enerji) alırken, iyonlaşma enerjisinin üzerinde ise elektron her enerji değerini (sürekli enerji) alabilir. Bu durumda elektronu atomdan koparmak için (atomu iyonlaştırmak için) gerekli enerji bağlanma enerjisi olup, toplam enerjinin zıt işaretlisine eşittir.

Ayrıca elektronların iyonlaşma enerjileri,

n=1 için 13,6 eV
n=2 için 3,4 eV
n=3 için 1,5 eV
n=∞ için 0 eV

Buradan, n büyüdükçe iyonlaşma enerjilerinin azaldığı görülür.

Hidrojen atomunda elektron yüksek enerjili (Ei) bir yörüngeden ( ni) düşük enerjili, (Es) bir yörüngeye (ns) geçerken yayılan elektromagnetik ışımanın frekansı,

$\displaystyle \upsilon =\frac{{{E}_{i}}-{{E}_{s}}}{h}$ olarak bulunur.

Yayılan ışığın dalga boyu ise,
$\displaystyle \frac{1}{\lambda }=\frac{\upsilon }{c}$

$\displaystyle \frac{1}{\lambda }=\frac{R}{hc}.\left( \frac{1}{n_{s}^{2}}-\frac{1}{n_{i}^{2}} \right)$

bağıntısından bulunur.

Burada,

R : joule
h : joule. saniye
c : m/s alındığında dalga boyu metre cinsinden çıkar.

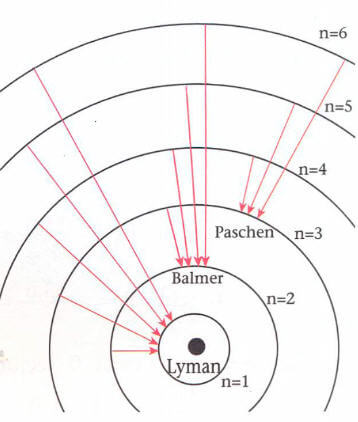hidrojen-atom-spektrumu-1 Elektronun değişik üst yörüngelerden, aynı alt yörüngeye doğrudan geçmesiyle yayılan ışımalar spektrum serilerini oluşturur.

1. Üst yörüngelerden n = 1 e doğrudan geçişler Lyman (morötesi ışınlar bölgesi) serisini oluşturur.
2. Üst yörüngelerden n = 2 ye doğrudan geçişler Balmer (görünür ışınlar bölgesi) serisini oluşturur.
3. Üst yörüngelerden n = 3 e doğrudan geçişler Paschen (kırmızı ötesi ışınlar bölgesi) serisini oluşturur.

$\displaystyle \alpha ,\beta ,\gamma ,...$ ile gösterilen geçişler Lyman serisini

$\displaystyle {{H}_{\alpha }},{{H}_{\beta }},{{H}_{\gamma }},....$ ile gösterilen geçişler Balmer serisini oluşturur. Bu serilerin frekans ve dalga boyları,

$\displaystyle \upsilon =\frac{R}{h}.\left( \frac{1}{n_{s}^{2}}-\frac{1}{n_{i}^{2}} \right)$

$\displaystyle \frac{1}{\lambda }=\frac{R}{hc}\left( \frac{1}{n_{s}^{2}}-\frac{1}{n_{i}^{2}} \right)$

ifadelerinden bulunur.

Bohr atom modeli; hidrojen ve hidrojene benzer tek elektronlu, mesela bir defa iyonlaşmış Helyum $\displaystyle {{\left( He \right)}^{+}}$ iki defa iyonlaşmış Lityum $\displaystyle \left( L{{i}^{++}} \right)$ , üç defa iyonlaşmış Bor $\displaystyle \left( {{B}^{+3}} \right)$ atomları için deney sonuçlarıyla uyumlu sonuçlar vermektedir. Ancak çok elektronlu atomların spektrumlarını açıklamakta yetersiz kalmıştır. Bu güçlük elektronların yerini ona eşlik eden de Broglie dalgası, yörüngelerin yerini de elektronların bulunma ihtimalinin en büyük olduğu küresel kabuklar şeklinde ifade eden kuantum mekaniği ile giderilmiştir. Ayrıca Bohr çok elektronlu atomların spektrumlarının ince yapı göstermesi yani herhangi bir spektrum çizgisinin birkaç çizgiye ayrılması, spektrum çizgilerinin parlaklıklarının farklı olması, elektronların kendi çevrelerinde de dönmesi (spin) gibi olayları açıklayamaz.