Hiperbol nedir, ne demektir? Hiperbol nasıl bir şekildir, nasıl çizilir, hiperbolün özellikleri nelerdir? Hiperbol hakkında bilgi.
Hiperbol Hakkında Bilgi
Hiperbol bir tür konik bölümdür. Diğer üç konik tipte olduğu gibi – paraboller, elipsler ve daireler – bir koninin ve bir düzlemin kesişiminden oluşan bir eğridir. Düzlem, bir çift koninin her iki yarısını kesiştiği ve tam olarak birbirine benzeyen, ancak ters yönlerde açılan iki eğri yaratacağı zaman bir hiperbol oluşturulur. Bu, koninin ekseni ile düzlem arasındaki açı, koninin yanındaki bir çizgi ile düzlem arasındaki açıdan daha az olduğunda meydana gelir.
Hiperbollar doğanın birçok yerinde bulunabilir. Örneğin, başka bir nesnenin etrafındaki açık yörüngede olan bir nesne bir hiperbol şeklinde hareket edebilir. Güneş saatinde, zamanla gölgenin ucu tarafından izlenen yol bir hiperboldur.
En iyi bilinen hiperbollerden biri, f (x) = 1 / x} denkleminin grafiğidir.
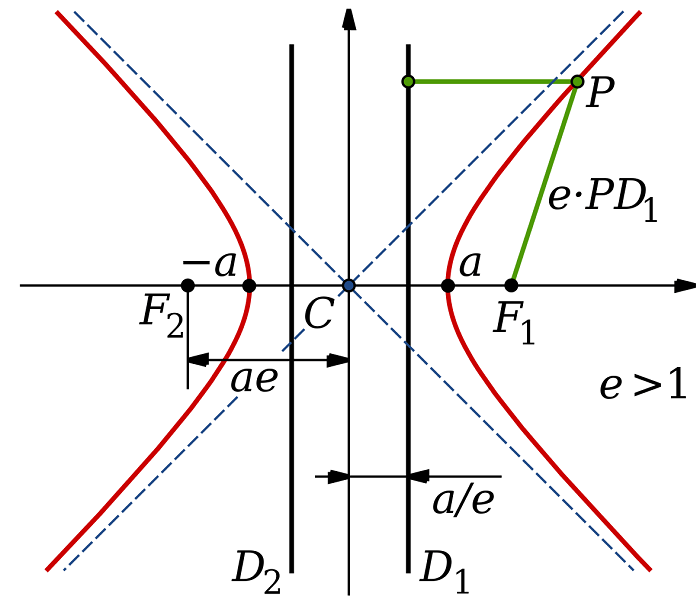
Hiperbollerin Özellikleri
Hiperbolde iki kesik eğri kol bulunur. Kolların birbirine en yakın olduğu iki noktaya tepe noktaları denir. Bu iki nokta arasındaki çizgi enine eksen veya ana eksen olarak adlandırılır. Enine eksenin orta noktası, hiperbolün merkezidir.
Merkezden uzak mesafelerde, hiperbolün kolları iki düz çizgiye yaklaşır. Bu iki satıra asimptotlar denir. Merkeze olan mesafe arttıkça, hiperbol asimptotlara yaklaşır, ancak kesişmez.
Eşlenik eksen veya küçük eksen, enine eksene dik açıdadır. Konjugat ekseninin uç noktaları, tepe noktasına kesişen ve enine eksene dik olan bir parçanın asimptotlarla kesiştiği yüksekliktedir.
Kartezyen koordinat sisteminin orijininde merkeze sahip, (0,0) noktası olan ve x ekseni üzerinde enine bir eksene sahip olan bir hiperbol denklemi şöyle yazılabilir.
a, merkez ile tepe arasındaki mesafedir. Enine eksenin uzunluğu 2a’ya eşittir. b, dikey bir çizgi bölümünün tepe noktasından asimptotuna kadar olan uzunluktur. Konjugat ekseninin uzunluğu 2b’ye eşittir.
Yukarıdaki hiperbol tipinin iki dalı sola ve sağa açılır. Dallar yukarı ve aşağı açılırsa ve enine eksen y eksenindeyse, hiperbol denklem şöyle yazılabilir.
KAYNAK 2
Hiperbol; Bir geometri şeklidir. Bir koniyi eksenine paralel olarak kesince ortaya çıkan kesit hiperboldür. Üzerindeki her noktanın, “odak” adı verilen iki noktaya olan uzaklıklarının farkı aynıdır. Bu uzaklık 2a ile, odaklar F harfiyle gösterilir. Odaklar arasındaki uzunluğa da 2c denir. 2a ve 2c bir hiperbolü belirten değerlerdir. Her hiperbolde bu değerler başka başkadır.
Hiperbolün iki kolu vardır. Bu iki kol birbirinin aynıdır. Bir koniyi düşey eksenine paralel olarak bir düzlemle kesersek hiperbolün kollarından birini elde ederiz. Hiperbolün kolları arasında çaprazlama çizilen iki çizgi vardır. Bunlara hiperbolün asimptot eksenleri denir. Bu eksenler ve hiperbolün kolları sonsuza kadar uzarlarsa da hiçbir zaman kesişemezler.