Hiperbol nedir, hiperbolün özellikleri nelerdir? Hiperbol soruları, örnek çözümleri, hiperbolün örneklerle konu anlatımı.
Hiperbol
Tanım Düzlemde sabit F1 ve F2 noktalarına uzaklıkları farkı sabit olan noktaların geometrik yerine hiperbol denir.
Sabit F1 ve F2 noktalarına hiperbolün odakları, [F1F2] nin orta noktasına da hiperbolün merkezi denir.
Merkezi orijinde ve odakları F1(-c, 0) ve F2(c, 0) olan hiperbolü inceleyelim.
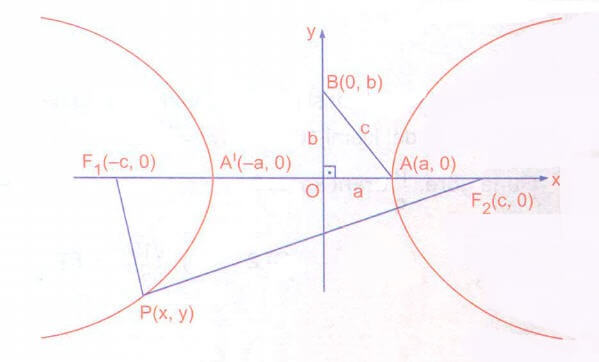
Hiperbolün üzerindeki değişken nokta P(x, y) olsun. P nin F1 ve F2 ye olan uzaklıkları farkını 2a alalım. Buna göre tanım gereği
|d(F1,P)-d(F2, p)| = 2a veya
||F1P|-|F2P|| = 2a olacaktır.
Bu durumda hiperbolün köşeleri olan A ve A’ nün koordinatları A(a, 0) ve A'(-a, 0) olur.
Yukarıdaki şekilde AOB dik üçgeninde pisogar bağıntısını kullanırsak
olur.
A(a, 0), B(0, b), A'(-a, 0) ve B'(0, – b) noktalarına hiperbolün köşeleri veya uç noktaları denir.
[AA1] na asal eksen denir.
|AA’| = 2a dır. (Odaklar daima asal eksen üzerindedir.) [BB1] na yedek eksen denir. |BB’| = 2b dir.
UYARI
Elipste asal eksen yedek eksenden büyüktür. Fakat hiperbolde böyle bir şart yoktur.
• Odakları arası uzaklık
|F1F2| = 2c dir.
• ||F1P| – |F2P|| = 2a ifadesini yukarıdaki şekle göre düzenlediğimizde köşeleri A(a, 0), B(0, b), A'(-a, 0)
ve B'(0, -b) olan hiperbolün standart denklemi
olarak elde ederiz.
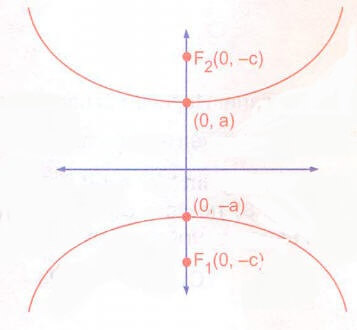
Odakları F1 (0, -c) ve F2(0, c) noktaları olan hiperbolün standart denklemi
dir.
Grafiği aşağıdaki gibidir.
ÖRNEK:
Merkezi orijinde asal ekseni X ekseninde, asal eksen uzunluğu 8 birim yedek eksen uzunluğu 10 birim olan hiperbolün odaklarını bulup standart denklemini yazınız?
Çözüm
2a = 8 ise a = 4
2b = 10 ise b = 5 tir.
c² = a² + b²
c² = 4² + 5² = 41
Bu duruma asal eksen X ekseninde olduğu için odakları ve
olur.
Denklemi:
ÖRNEK:
Merkezi orijinde asal eksen uzunluğu 6 birim ve odaklarından biri (-5, 0) olan hiperbolün standart denklemini yazınız?
Çözüm
Odağı (-5, 0) ise asal eksen X ekseninde ve c = 5 tir.
2a = 6 ise a = 3 tür.
olur.
Hiperbolün denklemi:
olur.
ÖRNEK:
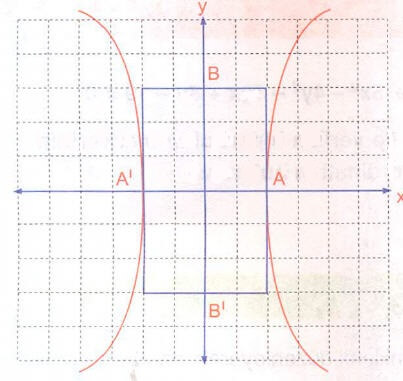
Düzlemsel şekil birimkarelerden oluşmaktadır.
Yukarıdaki koordinat sisteminde hiperbolün bazı temel elemanları verilmiştir.
Buna göre, hiperbolün standart denklemini yazınız?
Çözüm
Şekle göre hiperbolün uç noktaları A(2, 0), B(0, 3), A'(-2, 0) ve B'(0, – 3) tür.
O halde a = 2 ve b = 3 tür.
Asal ekseni x eksenindedir.
Denklemi:
olur.