İş Güç Enerji Detaylı Konu Anlatımı, Formüller ve Grafikleri

İş güç enerji nedir, kavramların açıklaması, formüllleri, özellikleri nelerdir? İş güç enerji konu anlatımı.Korunumlu Kuvvetler ve Mekanik Enerji Korunum

İş güç enerji

İŞ, GÜÇ, ENERJİ

İŞ (W):

İş sözcüğü günlük hayatımızda birçok anlamda kullanılan bir sözcüktür. Bununla beraber iş sözcüğü fizikte oldukça dar ve belirli anlamda kullanılır.

Fiziksel anlamda iş, bir kuvvet cisme etki ettiği zaman, cisim kuvvet etkisinde yer değiştirme yapıyorsa, kuvvetin cismin yerdeğiştirme doğrultusundaki bileşeni ile cismin yer değiştirmesi çarpımı olarak tanımlanır.

Cisim F kuvveti etkisinde ΔX kadar yerdeğiştiriyorsa yapılan iş W = F . ΔX bağıntısı ile bulunur.

Matematiksel bağıntıda F ve ΔX vektörlerinin skaler çarpımı işi verir.

Şekilde sürtünmesiz yatay bir düzlemde duran bir cisme dengelenmemiş, sabit bir kuvveti etki eder ve cisim F kuvvet etkisinde ΔX kadar yerdeğiştiriyorsa yapılan iş, W = F. ΔX bağıntısıyla verilir.

Burada kuvvet ile yerdeğiştirme aynı doğrultuda olduğu için vektör sembolleri kullanılmamıştır.

Eğer şekildeki gibi dengelenmemiş sabit F kuvveti, cismin yerdeğiştirme doğrultusundan farklı doğrultuda ise kuvvetin yerdeğiştirme doğrultusundaki bileşeni Fx fiziksel olarak iş yapar. Düşey bileşen doğrultusunda cisim yerdeğiştirme yapmadığı için fiziksel anlamda iş yapmaz. İş, w = F . ΔX vektörlerinin skaler çarpımı yerine,
W = Fx . ΔX yazılabilir.

Fx = F . Cos α olup, yerine konursa

W = F . ΔX . Cos α denklemi yapılan işi verir.

UYARI

★Kuvvet, cismin yerdeğiştirme doğrultusunda ve aynı yönde ise, yapılan iş pozitif (+) dır.

★Kuwet, cismin yerdeğiştirme doğrultusunda fakat zıt yönde ise, yapılan iş negatif (-) dir.

★Kuvvet cismin yerdeğiştirme doğrultusuna dik ise (α = 90°) yapılan iş sıfırdır.

★Bir cisim birden fazla kuvvetin etkisi altında yerdeğiştiriyorsa yapılan iş;

a) Kuvvetler aynı düzlemde ise kuvvetlerin bileşkesinin yaptığı işe eşittir.

b) Kuvvetler farklı düzlemlerde ise kuvvetlerin yerdeğiştirme doğrultusundaki bileşenlerinin yaptıkları işlerin cebirsel toplamına eşittir.

İŞ BİRİMLERİ: SI birim sisteminde

F = Newton (N) ve ΔX = metre, (m) dir.

İş birimi W = F . ΔX . Cos α denkleminden W = N . m olup bu birime joule (J) denir.

CGS sisteminde; F = Dyn ve ΔX = cm. alınırsa iş birimi W = dyn . cm olup bu birime Erg denir.
1j = 10 7 Erg dir.

DEĞİŞİK DURUMLARDA YAPILAN İŞ

A) Bir cismi düşey olarak kaldırmak için yapılan iş:

Bir cismin yerini düşey olarak değiştirmek için yapılan iştir. Kütlesi (m) olan bir cismi yerin çekim alanı içinde (h) yüksekliğine sabit bir F kuvveti ile sabit hızda kaldırmak için F kuvveti cismin G ağırlığına eşit ve zıt yönde olmalıdır.

W = G.h dir.
G = m.g
W = m.g.h. olur.

Bir eğik düzlemde (m) kütleli bir cismi (h) yüksekliğine çıkartmak için yapılan iş;

Cisme uygulanan F kuvveti Cismin G ağırlığının yerdeğiştirme doğrultusundaki bileşeni Fx ‘ye eşit ve zıt yönlü olmalıdır.

W = F.ΔX
F = Fx ve
Fx = G.Sinα yerine konursa,

$\displaystyle W={{F}_{x}}.\Delta X=G.\Delta X.Sin\alpha$ olur.

$\displaystyle Sin\alpha =\frac{h}{\Delta x}\Rightarrow \Delta x=\frac{h}{Sin\alpha }$

$\displaystyle W=G.\frac{h}{Sin\alpha }.Sin\alpha \Rightarrow W=G.h$

bulunur.

UYARI

Bir cismi (h) yüksekliğine kaldırmak için yapılan iş, cismin aldığı yoldan bağımsızdır. Yalnız cismin G ağırlığı ile (h) yüksekliğine bağlıdır. W = G . h

B) Sürtünme kuvvetlerinin yaptığı iş:

Sürtünme kuvveti cismin yerdeğiştirme yönüne daima zıt yönde olduğu için sürtünme kuvvetlerinin yaptığı iş daima (-) negatiftir.

$\displaystyle W=-{{F}_{r}}.\Delta X$
$\displaystyle {{F}_{r}}=k.N$
k = sürtünme katsayısı, N = Ağırlığın yüzeye dik bileşenidir. Wr = -k.N. ΔX

C) Hızlandırma İşi:

Sabit bir F kuvveti ile (m) kütleli bir cismi (a) ivmesiyle AX yerdeğiştirmesi boyunca hızlandırmak için yapılan iştir.

W = F.ΔX ve F = m.a olup, W = m.a.ΔX dır.

Hızlandırma işi, cismin kinetik enerji değişim miktarına eşittir.

D) Esnek şekil değiştirme işi:

Esnek bir yayı ΔX kadar germek veya sıkıştırmak için yapılan iştir.

Esneklik sabiti (k) olan bir yayı, sabit bir F kuvveti ile ΔX kadar uzatmak için yapılan iş;

F = k.ΔX olup
W = 1/2 F. ΔX =1/2 k. ΔX . ΔX
W = 1/2.k.ΔX² bulunur.

İşin hesaplanmasında, F kuvveti, ΔX ile orantılı olarak değiştiği için F’nin ortalama değeri alınır.

KUVVET-YERDEĞİŞTİRME GRAFİKLERİ

Kuvvet-yerdeğiştirme grafiklerinde, grafik çizgisi altında kalan alan, kuvvetin yaptığı işi verir. Grafik altında kalan alanlar hesaplanırken işaretler dikkate alınır.

GÜÇ

Günlük yaşantımızda ve teknolojide işin büyüklüğü yanında, işin yapılma süresi de önemlidir. Çoğu zaman bir kuvvetin iş yapma hızını da bilmek gerekir.

Birim zamanda yapılan işe güç denir. Δt süresince yapılan iş W ise güç,

$\displaystyle P=\frac{W}{\Delta t}$ bağıntısı ile verilir.

Bu ortalama gücün tanımıdır. Ani güç, küçük bir Δt zaman aralığında yapılan iş olup, P = F . v bağıntısı ile belirlidir. Güç kuvvet ile hız vektörünün skaler çarpımıdır. SI birim sisteminde W = Joule ve Δt = saniye olup, güç birimi P = joule/saniye = J/S = Watt (W) dır. Watt’ın üst birimleri:

I. Kilowatt (kW) = 10^3W

II. Megawatt (MW) = 10^6W dır. Mühendislikte güç birimi Beygir Gücü (BG) kullanılır. 1BG = 746W dır.

ENERJİ

Enerji herhangi bir sistemin iş yapabilme ‘ yeteneği olarak tanımlanır. Bir sistem enerjiye sahip ise başka bir sisteme etki edip, ona iş yaptırabilir. Bir barajda toplanan su, sıkıştırılmış bir çelik yay, depolanmış su buharı, hareket halinde bir cisim enerjiye sahiptir. Enerji yapılan veya yapılacak işle ölçüldüğünden enerji birimi joule dür. Doğada mekanik, ısı, ışık, elektrik, kimyasal ve nükleer enerji gibi çeşitli enerji biçimleri vardır.

ENERJİ ÇEŞİTLERİ

A) Kinetik Enerji (Ek):

Cisimlerin hareketinden dolayı sahip oldukları enerji çeşididir. Durmakta olan (m) kütleli bir cisme sabit bir F kuvveti uygulandığında bu kuvvet etkisinde cisim ΔX kadar yerdeğiştirdiğinde yapılan iş W = F . ΔX tir. Cisim bu kuvvet etkisiyle Newton’un II. yasasına göre,

a = F/m lik ivme kazanır. ΔX yerdeğiştirmesi sonunda cismin hızı v olur.

v² = 2 . a. ΔX bağıntısından
$\displaystyle a=\frac{{{v}^{2}}}{2.\Delta X}$ olur.

$\displaystyle W=F.\Delta X=m.a.\Delta X$ hızlandırma işinde ivme değeri yerine konursa,

$\displaystyle W=m.\frac{{{v}^{2}}}{2.\Delta X}.\Delta X=\frac{1}{2}m.{{v}^{2}}$ bulunur.

Cisim üzerine yapılan iş karşılığında cismin kazandığı (1/2 m . v²) niceliğine o cismin kinetik enerjisi denir.

$\displaystyle {{E}_{k}}=\frac{1}{2}m.{{v}^{2}}$

İş-Enerji Prensibi:

Bir kuvvet tarafından bir cisim üzerinde yapılan iş, cismin kinetik enerji değişimine eşittir.

$\displaystyle W=\Delta {{E}_{k}}$

$\displaystyle \Delta {{E}_{k}}=E_{k}^{'}-{{E}_{k}}=\frac{1}{2}m.{{v}^{'2}}-\frac{1}{2}m.{{v}^{2}}$

Kinetik enerji de iş gibi skaler bir niceliktir.

UYARI

*Cisim üzerine etkiyen F kuvveti, cismin hareket doğrultusunda ve hız vektörü ile aynı yönde ise yapılan iş (+) dir. Cismin kinetik enerjisi artar.

*F kuvveti cismin hareket doğrultusunda fakat hız vektörüne zıt yönde ise yapılan iş (-) olup, cismin kinetik enerjisi azalır.

B) Potansiyel Enerji

I- Yerçekimi Potansiyel Enerjisi: (Ep)

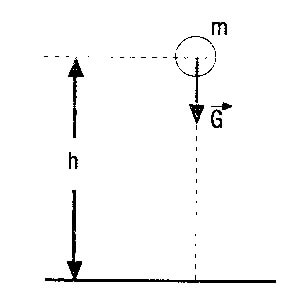
Şekilde (m) kütleli bir cisim (h) yüksekliğinden bırakıldığında yerçekimi kuvveti etkisiyle gittikçe hızlanarak yere düşer. Cisim (h) yüksekliğinden yere düşünce yerçekimi kuvveti bir iş yapar. O halde (h) yüksekliğinde bulunan cismin bir iş yapma kapasitesi vardır. Bir cismin yerin çekim alanı içinde bulunduğu konumdan dolayı sahip olduğu enerjiye çekim potansiyel enerji denir.

Bir cismi yerden (h) yüksekliğine çıkartmak için yapılan iş W = G . h = m.g.h dir. Yerçekimine karşı yapılan bu iş (h) yüksekliğine çıkartılan cisimde potansiyel enerji olarak depo edilir.

W = Ep = G . h = m.g.h

Burada cismin yeryüzündeki potansiyel enerjisi Ep = 0 alınmıştır. Çekim potansiyel enerjisi cismin bulunduğu (h) yüksekliğine bağlıdır. Bu nedenle potansiyel enerjinin değerini daima cismin bulunduğu yükseklik konumuna göre tanımlarız.

II- Esneklik Potansiyel Enerjisi:

Esnek bir yayın gerilmesi veya sıkıştırılmasıyla yayda depo edilen enerjidir.

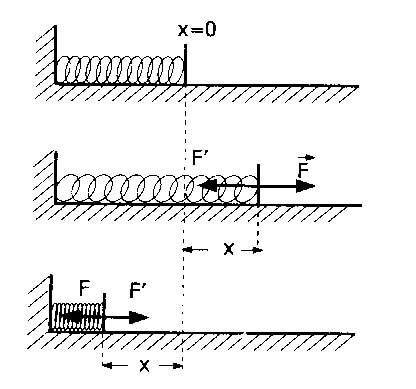
Şekilde esneklik sabit (k) olan bir yayın (x) kadar gerilmesi veya sıkıştırılması halinde yaya (x) uzama miktarıyla orantılı bir kuvvet uygulanır. F = F’ = -kx dir.

SI sisteminde k = N/m dir. Yayı (x) kadar germek veya sıkıştırmak için yapılan iş,

W = 1/2 F. x tir.

Bu iş yayda depo edilen esneklik potansiyel enerjiye eşittir. Bir yayın esneklik potansiyel enerjisi

W = Ep = 1/2 k. x² bağıntısıyla bulunur.

Korunumlu Kuvvetler ve Mekanik Enerji Korunum İlkesi:

Bir cismin sahip olduğu kinetik enerji ve potansiyel enerji toplamına mekanik enerji denir. E = Ek + Ep

Bir cismi, sabit bir F kuvveti etkisi altında A noktasından B noktasına farklı yollardan götürelim.

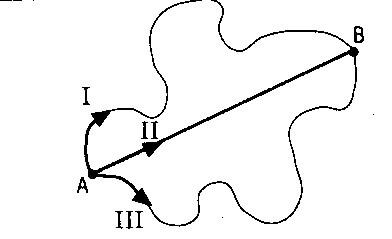
Genelde her yol boyunca F kuvvetinin yaptığı W1, W2 ve W3 işleri farklı olur.
$\displaystyle {{W}_{1}}\ne {{W}_{2}}\ne {{W}_{3}}$

Eğer iki nokta arasında her yol boyunca F kuvvetinin yaptığı işler birbirine eşit ise, yani yapılan işler izlenen yoldan bağımsız ise F kuvvetine korunumlu kuvvet denir.

W1 = W2 = W3 ise F korunumludur.

Örneğin;

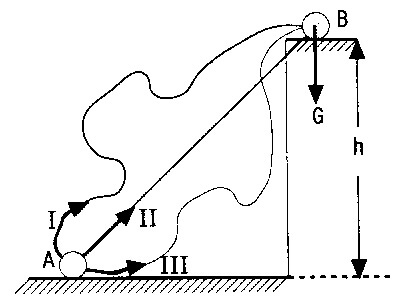
Şekildeki A noktasında bulunan cismi farklı yollardan (h) yüksekliğindeki B noktasına taşıyalım. Her yol boyunca yerçekifni kuvvetine karşı yapılan işler;

W1 = W2 = W3 = G.h dir.

Yapılan işler yoldan bağımsız olduğu için G yerçekimi kuvveti (ağırlık) korunumlu bir kuvvettir.

“Bir cisme etki eden bileşke kuvvet korunumlu ise cismin toplam mekanik enerjisi sabit kalır veya korunur.”

Buna mekanik enerji korunum ilkesi denir.

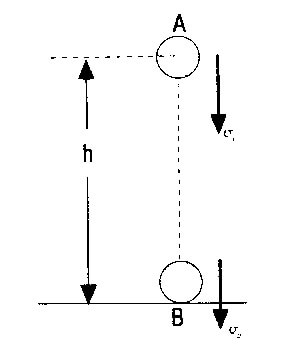
Bir cisim A noktasında iken kinetik enerjisi Ek ve potansiyel enerjisi Ep ise, korunumlu kuvvet etkisinde bir cisim için,

$\displaystyle E={{E}_{k}}+{{E}_{p}}=\frac{1}{2}m.v_{1}^{2}+mgh=sabit$

B noktasında,

$\displaystyle E={{E}^{'}}k+{{E}^{'}}p=\frac{1}{2}m.v_{2}^{2}+0=sabit$

Enerji korunum ilkesine göre,

$\displaystyle \Delta E=\Delta {{E}_{k}}+\Delta {{E}_{p}}\ne 0$ olur.

Yani, korunumlu olmayan kuvvet veya kuvvetlerin etkisi altında bulunan bir cismin toplam mekanik enerjisi sabit kalmaz veya korunmaz.

Korunumlu olmayan kuvvete karşı yapılan işten dolayı cismin harcadığı enerji Er ise,

$\displaystyle \Delta {{E}_{k}}+\Delta {{E}_{p}}=\Delta {{E}_{r}}$

$\displaystyle \Delta {{E}_{r}}$ korunumlu olmayan kuvvetler tarafından harcanan enerji, genelde ortamda ısı enerjisi olarak harcanır. Bu nedenle bir cismin toplam enerjisinin bir kısmı ısı enerjisine dönüşmüş olur.

* Yerçekimi kuvveti, esnek çarpışmalarda etkileşme kuvvetleri, elektrik kuvvetleri, esnek bir yaydaki geri çağırıcı kuvvet korunumlu kuvvetlerdir.

SERBEST DÜŞEN BİR CİSİMDE ENERJİ DÖNÜŞÜMÜ:

Havayla cisim arasındaki sürtünme ihmal edilirse (h) yüksekliğinde bulunan bir cismin yalnız Ep enerjisi vardır. Cisim serbest düşmeye bırakıldığında yerçekimi ivmesiyle hızlanır. Hızlanan cismin kinetik enerjisi artarken, yüksekliği azaldığı için Ep enerjisi azalır. Cisim yere çarptığı anda tüm Ep si Ek ya dönüşmüş olur. Cismin herhangi bir anda sahip olduğu mekanik enerji,

$\displaystyle E={{E}_{k}}+{{E}_{p}}=\frac{1}{2}m.{{v}^{'2}}+mg{{h}^{'}}=mgh$ dir.

Yani $\displaystyle \Delta {{E}_{k}}=-\Delta {{E}_{p}}$

ESNEK BİR YAY İLE BİR CİSMİN ETKİLEŞMESİNDE ENERJİ DÖNÜŞÜMÜ:

Yatay sürtünmesiz bir düzlemde (m) kütleli bir cisim (v) hızıyla esneklik sabiti (k) olan bir yaya çarptığında, başlangıçta sistemin toplam enerjisi, cismin kinetik enerjisine eşittir.

E = Ep + Ek = 0 + 1/2 m.v² (I)

Etkileşme başladığında cismin hızı yavaşladığı için kinetik enerjisi azalır. Yay sıkıştığı için esneklik potansiyel enerjisi artar. Sistemin toplam enerjisi

E = Ep + Ek = 1/2 kx² + 1/2 m.v’ ² olur (II)

Cisim durduğu zaman, yayda maksimum’ sıkışma olur. Cismin kinetik enerjisi sıfır, yayın potansiyel enerjisi maksimum olur. Sistemin toplam enerjisi

E = Ep + Ek = 1/2 kx²max + 0 = 1/2 m.v² (III)

Daha sonra yay cismi ters yönde itmeye başlar. Yayın sıkışma miktarı azaldığı için esneklik potansiyel enerjisi azalır. Cisim hızlandığı için kinetik enerjisi artar. Cisim yaydan ayrıldığı anda (etkileşmenin bitimi) cisim başlangıçtaki kinetik enerjisini tekrar kazanmış olur. Sistemin toplam enerjisi

E = Ep + Ek = 0 + 1/2 m.v² = 1/2 m.v² (IV) olur.