Advertisement
Karmaşık sayılar ve çember ilişkisi nedir, özellikleri nelerdir? Çözümlü örnek sorular ve karmaşık sayılar ve çember konu anlatımı.

KARMAŞIK SAYI VE ÇEMBER
ve
olmak üzere,
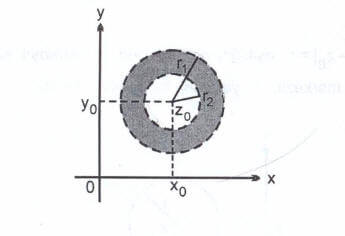
eşitliğini gerçekleyen z karmaşık sayıları
merkezli, r yarıçaplı bir çember belirtir.
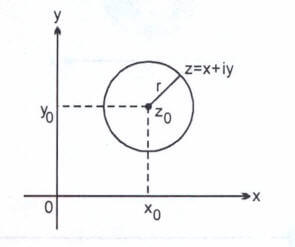
eşitliği
merkezli, r yarıçaplı çemberin iç bölgesidir.
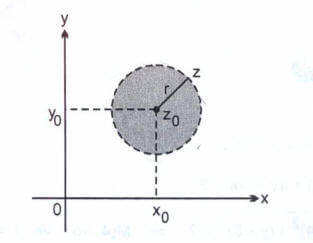
eşitsizliği
merkezli, r yarıçaplı çemberin dış bölgesidir.
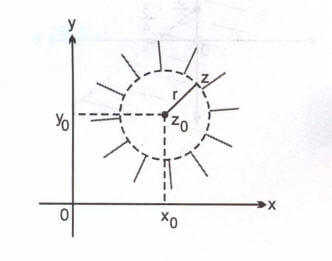
eşitsizliği bir halka belirtir.
Advertisement
Örnek:
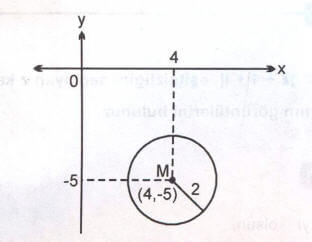
eşitliğini sağlayan z = x + iy karmaşık sayılarının geometrik yerinin denklemi ve karmaşık düzlemdeki görüntüsünü bulunuz.
Çözüm:
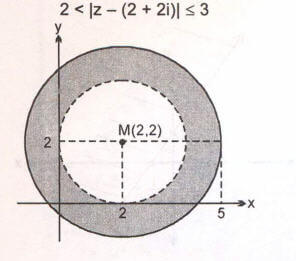
Örnek:
koşulunu sağlayan z = x + iy karmaşık sayılarının grafiğini karmaşık düzlemde gösteriniz.
Çözüm:
Örnek:
olmak üzere
sayısının alabileceği en küçük ve en büyük değerlerin toplamı kaçtır?
Çözüm:
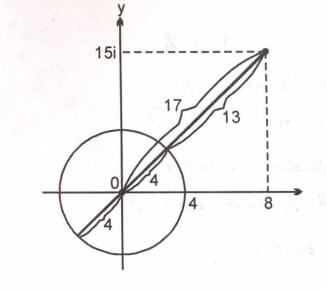
1. Yol
Advertisement
sayısının şekilde görüldüğü gibi alabileceği en küçük değer 13, en büyük değer 21 dir. 13 + 21 =34 tür.
2. yol:
olduğunu hatırlayalım.
olduğuna göre, en küçük değer 13, en büyük değer 21 dir. 13 + 21 =34 tür.
Örnek:
A kümesinin karmaşık düzlemdeki görüntüsü nedir?
Çözüm:
olsun.
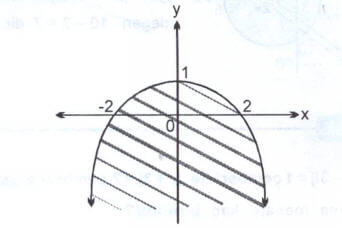
Örnek:
bağıntısının karmaşık düzlemdeki görüntüsü nedir?
Çözüm:
olsun
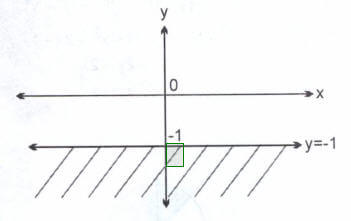
Örnek:
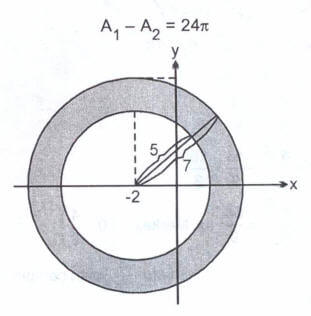
eşitsizliğinin belirttiği bölgenin alanını bulunuz.
Çözüm: