Karmaşık Sayıların Kutupsal Yazılımında İşlemler

Karmaşık sayıların kutupsal olarak yazılımında toplama, çıkarma, çarpma ve bölme işlemi, örnek, çözümlü sorular.

Karmaşık Sayıların Kutupsal Yazılımında İşlemler

1. TOPLAMA VE ÇIKARMA

$\displaystyle {{z}_{1}}=\sqrt{2}\left( \cos 45{}^\circ +i.\sin 45{}^\circ \right)$

$\displaystyle {{z}_{2}}=2\left( \cos 150{}^\circ +i.\sin 150{}^\circ \right)$

$\displaystyle {{z}_{1}}+{{z}_{2}}$ ve $\displaystyle {{z}_{1}}-{{z}_{2}}$ sayılarını bulmak için önce karmaşık sayılar standart biçime dönüştürülür.

$\displaystyle {{z}_{1}}=\sqrt{2}.\left( \frac{\sqrt{2}}{2}+i\frac{\sqrt{2}}{2} \right)=1+i$

$\displaystyle {{z}_{2}}=2.\left( -\frac{\sqrt{3}}{2}+i\frac{1}{2} \right)=-\sqrt{3}+i$

$\displaystyle {{z}_{1}}+{{z}_{2}}=\left( 1+i \right)+\left( -\sqrt{3}+i \right)=\left( 1-\sqrt{3} \right)+2i$

$\displaystyle {{z}_{1}}-{{z}_{2}}=\left( 1+i \right)-\left( -\sqrt{3}+i \right)=\left( 1+\sqrt{3} \right)+0.i=1+\sqrt{3}$

2. ÇARPMA

$\displaystyle {{z}_{1}}={{r}_{1}}.cis\theta$

$\displaystyle {{z}_{2}}={{r}_{2}}.cis\alpha$

$\displaystyle {{z}_{1}}.{{z}_{2}}={{r}_{1}}.{{r}_{2}}.cis\left( \theta +\alpha \right)$

3. BÖLME

$\displaystyle \frac{{{z}_{1}}}{{{z}_{2}}}=\frac{{{r}_{1}}}{{{r}_{2}}}.cis\left( \theta -\alpha \right)$

Örnek:

$\displaystyle {{z}_{1}}=3.cis\frac{5\pi }{6}$ ve $\displaystyle {{z}_{2}}=5.cis\frac{\pi }{6}$ olduğuna göre, $\displaystyle {{z}_{1}}.{{z}_{2}}$ kaçtır?

Çözüm:

$\displaystyle {{z}_{1}}.{{z}_{2}}=\left( 3.cis\frac{5\pi }{6} \right).\left( 5.cis\frac{\pi }{6} \right)=15.cis\left( \frac{5\pi }{6}+\frac{\pi }{6} \right)$

$\displaystyle =15.cis\pi =15.\left( \cos \pi +i\sin \pi \right)=-15$

Örnek:

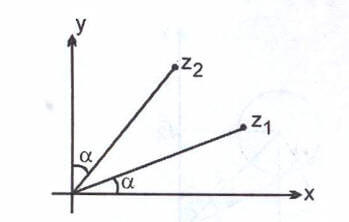
karmasik-sayilar-kutupsal-islemler-1

Şekilde $\displaystyle {{z}_{1}}$ ve $\displaystyle {{z}_{2}}$ karmaşık sayılarının karmaşık düzlemdeki yeri gösterilmiştir. $\displaystyle \left| {{z}_{1}} \right|=2$ $\displaystyle \left| {{z}_{2}} \right|=2$ Buna göre $\displaystyle {{z}_{1}}.{{z}_{2}}$ kaçtır?

Çözüm:

$\displaystyle {{z}_{1}}=2.cis\alpha$
$\displaystyle {{z}_{2}}=2.cis\left( 90{}^\circ -\alpha \right)$

$\displaystyle {{z}_{1}}.{{z}_{2}}=\left( 2.cis\alpha \right).\left( 2.cis\left( 90{}^\circ -\alpha \right) \right)=4.cis90{}^\circ$
$\displaystyle =4.\left( \cos 90{}^\circ +i\sin 90{}^\circ \right)=4i$

Örnek:

$\displaystyle {{z}_{1}}=2cis85{}^\circ$
$\displaystyle {{z}_{2}}=cis25{}^\circ$

olduğuna göre, $\displaystyle \left| {{z}_{1}}-{{z}_{2}} \right|$ kaçtır?

Çözüm:

$\displaystyle \left| {{z}_{1}}-{{z}_{2}} \right|$ ifadesi $\displaystyle {{z}_{1}}$ ve $\displaystyle {{z}_{2}}$ karmaşık sayıları arasındaki uzaklıktır.

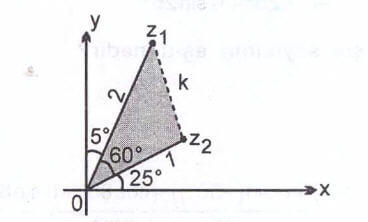
karmasik-sayilar-kutupsal-islemler-2

Taralı üçgende cosinüs teoremi kullanılırsa;

$\displaystyle {{k}^{2}}={{2}^{2}}+{{1}^{2}}-2.2.1\cos 60{}^\circ$
$\displaystyle {{k}^{2}}=4+1-2.2.\frac{1}{2}\Rightarrow {{k}^{2}}=3\Rightarrow k=\sqrt{3}$

Örnek:

$\displaystyle z=1+\cos 40{}^\circ +i.\sin 40{}^\circ$ olduğuna göre Arg(z) kaç radyandır?

Çözüm:

$\displaystyle z=1+\cos 40{}^\circ +i.\sin 40{}^\circ$

$\displaystyle z=1+2{{\cos }^{2}}20{}^\circ -1+i.2\sin 20{}^\circ \cos 20{}^\circ$

$\displaystyle z=2\cos 20{}^\circ .\left( \cos 20{}^\circ +i.\sin 20{}^\circ \right)=2\cos 20{}^\circ cis20{}^\circ$

Buradan $\displaystyle Arg\left( z \right)=20{}^\circ =\frac{\pi }{9}$ radyandır.

Örnek:

$\displaystyle z=1-\cos 20{}^\circ +i.\sin 20{}^\circ$ olduğuna göre, Arg(z) kaç derecedir?

Çözüm:

$\displaystyle z=1-\cos 20{}^\circ +i.\sin 20{}^\circ$

$\displaystyle z=1-1+2{{\sin }^{2}}10{}^\circ +i.2\sin 10{}^\circ \cos 10{}^\circ$

$\displaystyle z=2\sin 10{}^\circ .\left( \sin 10{}^\circ +i.\cos 10{}^\circ \right)$

$\displaystyle z=2\sin 10{}^\circ .\left( \cos 80{}^\circ +i.\sin 80{}^\circ \right)=2\sin 10{}^\circ .cis80{}^\circ$

Buradan $\displaystyle Arg(z)=80{}^\circ$

Örnek:

$\displaystyle z=\frac{\left( \cos 50{}^\circ -i.\sin 50{}^\circ \right).\left( \sin 5{}^\circ +i.\cos 5{}^\circ \right)}{-\cos 25{}^\circ +i.\sin 25{}^\circ }$ olduğuna göre, z karmaşık sayısının eşiti nedir?

Çözüm:

$\displaystyle z=\frac{\left( \cos 50{}^\circ -i.\sin 50{}^\circ \right).\left( \sin 5{}^\circ +i.\cos 5{}^\circ \right)}{-\cos 25{}^\circ +i.\sin 25{}^\circ }$

$\displaystyle z=\frac{cis\left( -50{}^\circ \right).cis85{}^\circ }{-\left( \cos \left( -25{}^\circ \right)+i.\sin \left( -25{}^\circ \right) \right)}$