Küre Yüzeyinin Denklemi Nedir? Hesaplanması, Örnek Soru ve Çözümleri

0

By gurur on 25 Şubat 2022 Matematik

Advertisement

Küre yüzeyinin denklemi nedir, denklem nasıl hesaplanır? Küre yüzeyinin denklemi ile ilgili örnek sorular ve bu soruların denklemlerle çözümü

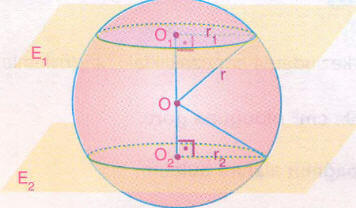
Küre Kuşağı

Küre Yüzeyinin Denklemi

XYZ dik koordinat düzleminde, merkezi 0(0, 0, 0) ve yarıçapı r olan küre yüzeyinin denklemi,

x² + y² + z² = r² dir.

Merkezi M(a, b, c) ve yarıçapı r olan küre yüzeyinde P(x, y, z) noktası alalım.

| PM | = r olacağından, iki nokta arasındaki uzaklık formülünden, küre yüzeyinin denklemi,
$\displaystyle {{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}+{{\left( z-c \right)}^{2}}={{r}^{2}}$ olur.

Örnek – 1

Merkezi 0(0, 0, 0) ve yarıçapı 5 birim oları kürenin denklemini yazalım. Eksenleri kestiği noktaları bulalım.

Çözüm

Advertisement

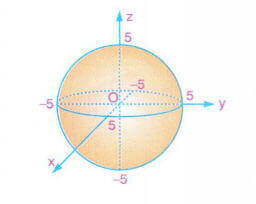
Küre Örnek Soru ve Çözümü

Kürenin denklemi,

$\displaystyle {{x}^{2}}+{{y}^{2}}+{{z}^{2}}={{5}^{2}}$
$\displaystyle {{x}^{2}}+{{y}^{2}}+{{z}^{2}}=25$ olur.
Küre yüzeyinin eksenleri kestiği noktaların koordinatları,
(5, 0, 0), (-5, 0, 0), (0, 5, 0), (0, -5, 0), (0, 0, 5), (0, 0, -5) olur.

Örnek – 2

Uzayda, A(3, 5, 4) ve B(-5, 3, 2) noktaları veriliyor. Buna göre, [AB] yi çap kabul eden küre yüzeyinin denklemini bulalım.

Çözüm

[AB] nin orta noktası M olsun. M, kürenin merkezidir.
$\displaystyle M\left( \frac{3-5}{2},\frac{5+3}{2},\frac{4+2}{2} \right)$
M(-1, 4, 3) olur.
|AB| nin yarısı kürenin yarıçapıdır.
$\displaystyle \left| AB \right|=\sqrt{{{\left( 3+5 \right)}^{2}}+{{\left( 5-3 \right)}^{2}}+{{\left( 4-2 \right)}^{2}}}$
$\displaystyle \left| AB \right|=\sqrt{64+4+4}=\sqrt{72}=6\sqrt{2}$ birim
$\displaystyle r=\frac{\left| AB \right|}{2}=3\sqrt{2}$ birim bulunur.

Buna göre, küre yüzeyinin denklemi,

$\displaystyle {{\left( x+1 \right)}^{2}}+{{\left( y-4 \right)}^{2}}+{{\left( z-3 \right)}^{2}}={{\left( 3\sqrt{2} \right)}^{2}}$
$\displaystyle {{\left( x+1 \right)}^{2}}+{{\left( y-4 \right)}^{2}}+{{\left( z-3 \right)}^{2}}=18$ bulunur.

Not:

$\displaystyle {{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}+{{\left( z-c \right)}^{2}}={{r}^{2}}$
$\displaystyle {{x}^{2}}+{{y}^{2}}+{{z}^{2}}-2ax-2by-2cz+{{a}^{2}}+{{b}^{2}}+{{c}^{2}}-{{r}^{2}}=0$

Denklemde,

-2a = D, -2b = E, -2c = F ve
$\displaystyle {{a}^{2}}+{{b}^{2}}+{{c}^{2}}-{{r}^{2}}=G$ dersek, genel küre denklemi,
$\displaystyle {{x}^{2}}+{{y}^{2}}+{{z}^{2}}+Dx+Ey+Fz+G=0$ olur.

Örnek – 3

Denklemi, x² + y² + z² + 6x – 4y – 2z + 5 = 0 olan kürenin merkezi ve yarıçapını bulalım.

Çözüm

M(a, b, c) için,
$\displaystyle a=-\frac{D}{2}=-\frac{6}{2}=-3$
$\displaystyle b=-\frac{E}{2}=-\frac{4}{2}=2$
$\displaystyle c=-\frac{F}{2}=-\frac{2}{2}=1$
M(-3, 2, 1) olur.
$\displaystyle G={{a}^{2}}+{{b}^{2}}+{{c}^{2}}-{{r}^{2}}$
$\displaystyle 5=9+4+1-{{r}^{2}}$
$\displaystyle {{r}^{2}}=9\Rightarrow r=3$ birim bulunur.

Not

(x – a)² + (y – b)² + (z – c)² = r² denklemi küre yüzeyini belirtir.

Advertisement

(x – a)² + (y – b)² + (z – c)² < r² eşitsizliği kürenin iç bölgesindeki noktaları belirtir. (x – a)² + (y – b)² + (z – c)² > r² eşitsizliği kürenin dış bölgesindeki noktaları belirtir.

Örnek – 4

A(3, 2, -1) noktasının,
(x – 3)² + (y + 1)² + (z + 5)² = 16 küre yüzeyinin uzayda ayırdığı bölgelerden hangisinin elemanı olduğunu bulalım.

Çözüm

A(3, 2, -1) noktasını denklemde yerine yazalım. (3 – 3)² + (2 + 1)² + (-1 + 5)² = 16
O + 9 + 16 > 16 olduğundan, A noktası küre yüzeyinin dış bölgesindedir.

Leave A Reply Cancel Reply