Matematikte Sonsuz Kavramı

Matematikte sonsuz kavramı nedir, nasıl açıklanır? Matematiksel çözümlemede sonsuz, hesabı, hakkında bilgi.

Matematikte Sonsuz Kavramı

Soyut sonsuz kavramı iki bin yıl boyunca metafizik tartışmalara yol açtı. XIX. yy’dan sonra sonsuz, anlamsızlıktan yoksun matematiksel tanımlamaların konusu oldu.

SONSUZ

Sonsuz, matematiksel çözümlemede değişken bir niceliğin, önceden belli her değişmez niceliği geçtiği problemlerde ortaya çıkar. Sözgelimi, kesinlikle pozitif bir nicelik istendiği kadar

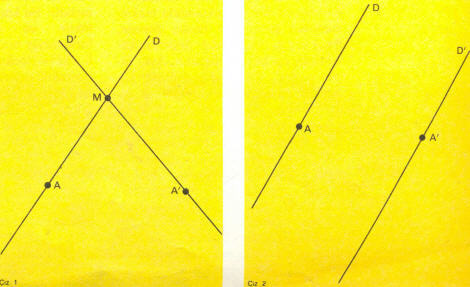
O’a yaklaşırsa, tersi , ne kadar büyük olursa olsun, verilen her gerçek sayıyı geçer. x sıfıra giderken f(x)’in sonsuz bir limiti olduğu söylenir. Böylece, R gerçek sayılar kümesine, sırasıyla + ∞ ve -∞(artı sonsuz ve eksi sonsuz diye okunur) ile gösterilen iki öğe katılmış olur. Sonsuzdaki öğeler gerçek sayıların hemen hemen bütün özelliklerini taşıdıklarından, sonsuz limitler bu durumda, öbürleri gibi limitler olur. (Bununla birlikte, + ∞ ile – ∞ toplamı ve O’m + ∞ ile çarpımı tanımlanamaz.) Sonsuz kavramı geometride paralel doğrular konusunda ortaya çıkar. İki sabit A ve A’ noktalarından geçen iki D ve D’ doğrusunu göz önüne alalım (Çiz. 1). Genel olarak bu doğruların bir ve yalnızca bir M ortak noktası vardır. D’ doğrusunu A’ çevresinde, D’ye paralel olana kadar çevirelim (Çiz. 2). M’nin A’ya uzaklığı gitgide büyük olur. Paralel D ve D’ doğrularının kesitleri, sonsuzdaki bir nokta olduğundan dolayı kesiştiklerini düşünmek uygun olur. Böylelikle, yöndeş doğrularla ya da paralel doğrularla ilgili bazı problemler aynı anda ele alınabilir.

Sonsuzdaki noktalar, sonsuzdaki doğrular, sonsuzdaki düzlemler, vb., 1822’de, j.V. Poncelet tarafından biçimlendirilen izdüşüm geometrisi çerçevesinde yer aldılar. Günümüzde, izdüşüm geometrisi, doğrusal cebirin gitgide önemsenmeyen bir bölümüdür. Yukarıda incelenen analitik ve geometrik görüşler birbirlerine sıkı sıkıya bağlıdırlar. Aynı bir topoloji probleminin iki görünüşü, yani belli bir yerdeki kompakt bir uzamın kompaktifikasyonu söz konusudur. Buna karşılık, kümeler kuramında kullanılan sonsuz kavramının yukarıdaki görüş noktasıyla yalnızca adı ortaktır. Cisimler sezgisel olarak, sayılabilir: Sıfır taş, bir taş, iki taş, üç taş, vb., “sonsuza kadar”, yani “en sona kadar” gitmeden sayılabilir. Doğal tamsayılar kümesi sonsuzdur denir. Sorun, böyle bir kümenin öğelerinin “sayısını” tanımlamaktır. Sonsuz kümelerin incelenmesi Georg Cantor tarafından ele alınmıştır. (Kümelerkuramının açıkça bu özel araştırmanın gereksiniminden ortaya çıkarıldığını da bu arada belirtelim.] Temel araçlar, sıral sayılar ve kardinal (sayal) sayılardır.