Su Dalgalarında Kırılma Konu Anlatımı

Su Dalgalarının kırılması nasıl olur? Su dalgalarında kırılma konu anlatımı, formüller, hakkında bilgi.

SU DALGALARINDA KIRILMA

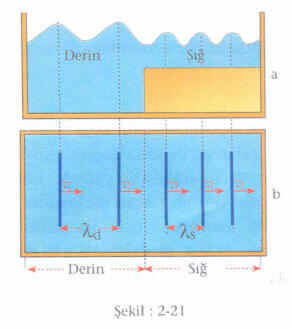
Dalgaların yayılma hızlarının değişik ortamlarda farklı olduğunu daha önce söylemiştik. Su dalgaları için yayılma hızı suyun derinliğine bağlıdır. Bu nedenle, farklı derinliklerde olan su, dalgaların yayılmasında farklı iki ortam gibi düşünülebilir. Dalga leğenindeki suyun bir kısmının dibine cam konularak farklı derinlikte iki ortam elde edilebilir. Bu iki ortamda dalgaların nasıl davrandıklarını inceleyebiliriz. Yayılma hızının suyun derinliğine bağlı olduğunu görmek için ortamları ayıran yüzeye paralel ve doğrusal dalgalar gönderelim. Şekil:2-21. a su ortamlarının yandan görünüşü, Şekil: 2-21 b ise dalgaların üstten görünüşüdür. (Yani tabandaki desen) Bu dalgalara stroboskopla baktığımızda stroboskobu uygun frekansta döndürürsek her iki bölgedeki dalgaları duruyormuş gibi görebiliriz. Her iki bölgedeki dalgaların frekansları eşittir ve bu frekans suyun derinliğine bağlı değildir. Dalganın frekansı kaynağın frekansına eşittir. Kaynakta bir değişiklik olmadığı sürece dalga ister sığ ortamda olsun, ister derin ortamda frekans değişmez ve aynı kalır. Kaynağın frekansı değişirse dalgaların da frekansı ancak o zaman değişir.

su-dalgalari-2-21

Sığ ortamdaki dalga boyu $\displaystyle \left( {{\lambda }_{s}} \right)$ , derin ortamdaki dalga boyundan $\displaystyle \left( {{\lambda }_{d}} \right)$ daha küçüktür.

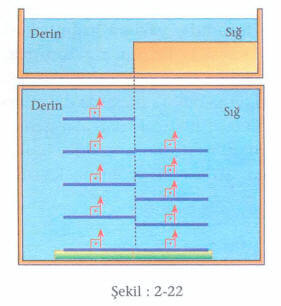
su-dalgalari-2-22

Ortam değiştiren dalgaların frekansı her iki ortam için de aynıdır. $\displaystyle {{\lambda }_{d}}>{{\lambda }_{s}}$ olduğundan $\displaystyle \vartheta =\lambda .f$ bağıntısına göre sığ ortamdaki dalga hızı $\displaystyle \left( {{\vartheta }_{s}} \right)$ derin ortamdaki dalga hızından $\displaystyle \left( {{\vartheta }_{d}} \right)$ daha küçüktür. (Şekil: 2-22)

$\displaystyle {{\vartheta }_{derin}}>{{\vartheta }_{s\imath g}}$

Buna göre dalgaların hızı derin ortamdan sığ ortama geçtiğinde azalacaktır. Frekans sabit olduğundan dalga boyu da azalacaktır. Aşağıda derinlik durumuna göre dalgaların üstten ve yandan görünüşleri çizilmiştir. (Şekil: 2-23)

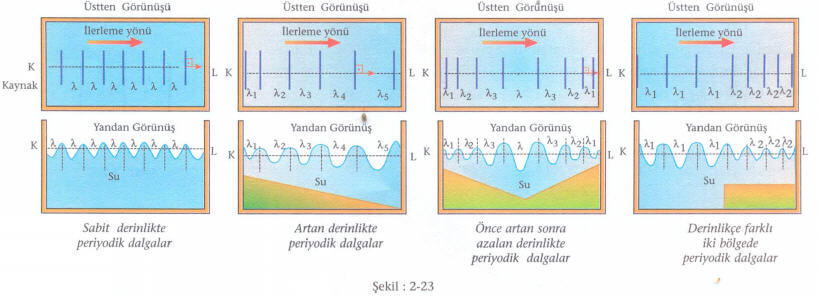
su-dalgalari-2-23

Derin ve sığ ortamları ayıran yüzey periyodik doğrusal dalgalara paralel ise, dalgaların ikinci ortamdaki ilerleme doğrultusu değişmez. Paralel değilse ikinci ortamdaki ilerleme doğrultusu değişir.

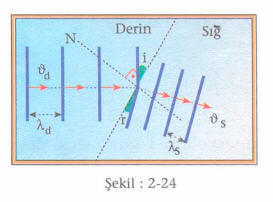
su-dalgalari-2-24

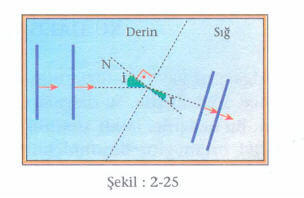
su-dalgalari-2-25

Şekil:2-24 de görüldüğü gibi derin ortamdan gelen periyodik doğrusal dalgalar sığ ortama geçtiklerinde yayılma doğrultuları değişmiştir. Gelen dalgaların arakesitle yaptığı i açısı gelme açısına, kırılan dalgaların arakesitle yaptığı r açısı da kırılma açısına eşittir. Işık, ortam değiştirdiğinde, geliş açısının sinüsü ile kırılma açısının sinüsü arasında sabit bir oran vardı. Acaba su dalgaları için de böyle bir kural var mıdır? Bunu anlamak için Şekil: 2-26 yı inceleyelim.

su-dalgalari-2-26

$\displaystyle \overset{\Delta }{\mathop{ABC}}\,\Rightarrow \sin i=\frac{\left| AC \right|}{\left| AB \right|}=\frac{{{\lambda }_{d}}}{\left| AB \right|}$

$\displaystyle \overset{\Delta }{\mathop{ABD}}\,\Rightarrow \sin r=\frac{\left| BD \right|}{\left| AB \right|}=\frac{{{\lambda }_{s}}}{\left| AB \right|}$

bulunur. Bu iki eşitlik taraf tarafa oranlanırsa;

$\displaystyle \frac{\sin i}{\sin r}=\frac{{{\lambda }_{d}}/\left| AB \right|}{{{\lambda }_{s}}/\left| AB \right|}$

$\displaystyle \frac{\sin i}{\sin r}=\frac{{{\lambda }_{d}}}{{{\lambda }_{s}}}$

bağıntısı bulunur. Buradaki gelme açısı i değiştirildiğinde buna karşılık ölçülen kırılma açısı r için bu oranın sabit olduğu görülmüştür. Bu sabit sayıya ikinci ortamın birinci ortama göre kırılma indisi adı verilir.

Buna göre,

$\displaystyle \frac{\sin i}{\sin r}={{n}_{1,2}}$

elde edilir.

Bu bağıntının dalga hızlarıyla ilişkisi ise,

$\displaystyle {{\lambda }_{d}}=\frac{{{\vartheta }_{d}}}{f}$

$\displaystyle {{\lambda }_{s}}=\frac{{{\vartheta }_{s}}}{f}$

değerleri yerine yazılırsa,

$\displaystyle {{n}_{1,2}}=\frac{\sin i}{\sin r}=\frac{{{\lambda }_{d}}}{{{\lambda }_{s}}}=\frac{{{\vartheta }_{d}}}{{{\vartheta }_{s}}}$

olarak bulunur. Eğer dalgalar sığ ortamdan derin ortama gelirse yukarıdaki bağıntıda dalga boylarının ve hızların oranlan ters döner. Çünkü sığdan derine geçerse i < r olur ve sini < sinr olur.

Bu formüle göre derinlik azaldığında, hız, dalga boyu ve kırılma açısı azalır.

Not: Su çok derin olmamak şartıyla yukarıdaki oranlar derinliklerin kareköküyle de doğru orantılıdır.

SONUÇ:

Su dalgalarının kırılmasını ışığın kırılmasına benzetebiliriz. Su dalgası derin ortamda hızlı, sığ ortamda yavaş olduğundan, derin ortam az kırıcı, sığ ortam ise çok kırıcı ortam gibi davranır.

Dolayısıyla derinden sığa geçen dalgaların ilerleme doğrultusu normale yaklaşırken sığdan derine geçen dalgaların ilerleme doğrultusu normalden uzaklaşır. Normal, derin ve sığ ortamları ayıran yüzeye diktir

Verilen herhangi iki ortam için ışık hızı ve kırıcılık indisi arasında ilişkinin tarihsel gelişimi şöyledir:

Newton (1669) ışığın tanecik teorisini geliştirerek,

$\displaystyle {{n}_{1,2}}=\frac{{{\vartheta }_{2}}}{{{\vartheta }_{1}}}$

olmalı dedi. Huygens’in(1678) ileri sürdüğü dalga modeli ise Newton’un söylediğinin tam tersiydi yani,

$\displaystyle {{n}_{1,2}}=\frac{{{\vartheta }_{1}}}{{{\vartheta }_{2}}}$

olduğunu öne sürüyordu. 1862 yılında Foucault, ışığın hızının suda havadakinden daha küçük olduğunu ölçtü. 1883 yılında da Michelson Morley tarafından,

$\displaystyle \frac{{{\vartheta }_{hava}}}{{{\vartheta }_{su}}}=1,33$

olduğu deneylerle gerçekleştirildi. Bu değer suyun havaya göre kırılma indisidir. Öyleyse ışığın saydam ortamlardaki hızı dalga modeliyle açıklanabilirken tanecik modeli ile açıklanamamaktadır.