Sürtünmeli ve Sürtünmesiz Yüzeylerde Hareket Formülleri

Yatay ve eğik sürtünmeli ve sürtünmesiz düzlemlerde hareket nasıl olur, formülleri ve açıklamaları. Sürtünme kuvveti formülleri.

Sürtünmeli Yüzeylerde Hareket Formülleri

Yatay Sürtünmesiz Düzlemde Hareket

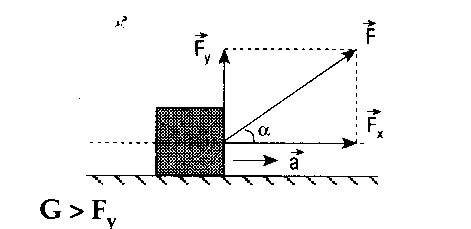
Şekilde $\displaystyle \overset{\to }{\mathop{F}}\,$ kuvvetinin düşey bileşeni yönünde bir hareket olmadığı için Fy’nin cismin ivmesi üzerine etkisi yoktur. Cisme ivme kazandıran kuvvet, $\displaystyle \overset{\to }{\mathop{F}}\,$ kuvvetinin yatay bileşeni Fx dir.

$\displaystyle {{F}_{x}}=\overset{\to }{\mathop{F}}\,.Cos\alpha$ olup

Dinamiğin temel kanununa göre;

$\displaystyle \sum \overset{\to }{\mathop{F}}\,={{F}_{x}}=m.\overset{\to }{\mathop{a}}\,\Rightarrow F.Cos\alpha =m.a$

$\displaystyle \overset{\to }{\mathop{a}}\,=\frac{F.Cos\alpha }{m}$ bulunur.

Yatay Sürtünmeli Bir Yüzeyde Hareket

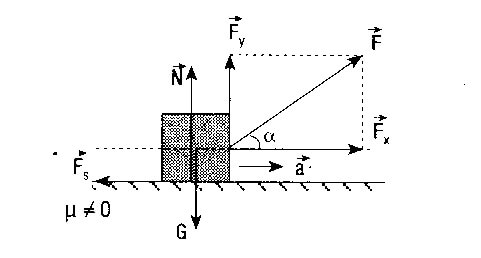
$\displaystyle \overset{\to }{\mathop{F}}\,$ kuvvetinin düşey bileşeni $\displaystyle {{F}_{y}}$ yüzey ile cisim arasındaki sürtünme kuvvetinin büyüklüğünü etkiler.

Cisme etki eden bileşke net kuvvet

$\displaystyle \sum F={{F}_{x}}-{{F}_{s}}$
$\displaystyle {{F}_{x}}=F.Cos\alpha$
$\displaystyle {{F}_{s}}=\mu .N$
$\displaystyle N=G-{{F}_{y}}$ olup
$\displaystyle \sum F={{F}_{x}}-\mu \left( G-{{F}_{y}} \right)$ olur.
$\displaystyle {{F}_{y}}=F.\sin \alpha$
$\displaystyle m.a=F.Cos\alpha -\mu \left( m.g.F.Sin\alpha \right)$
$\displaystyle \overset{\to }{\mathop{a}}\,=\frac{F.Cos\alpha -\mu \left( m.g-F.Sin\alpha \right)}{m}$

bulunur.

Sürtünmesiz Eğik Düzlemde Hareket

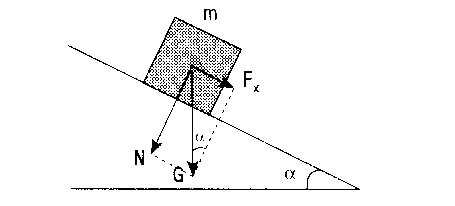
Sürtünmesiz eğik düzlemde cismin ağırlığı G’nin düzlem yüzeyine paralel bileşeni Fx cisme a ivmesi kazandırır.

$\displaystyle {{F}_{x}}=G.Sin\alpha =m.g.Sin\alpha$
$\displaystyle \sum F={{F}_{x}}$
$\displaystyle \sum F=m.a=m.g.Sin\alpha$
$\displaystyle a=g.Sin\alpha$ bulunur.

Sürtünmeli Eğik Düzlemde Hareket

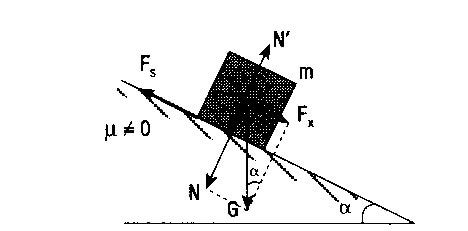
Cismin hareket edebilmesi için Fx > Fs olmalıdır. Cisme etki eden bileşke kuvvet

$\displaystyle \sum F={{F}_{x}}-{{F}_{s}}$
$\displaystyle {{F}_{x}}=G.Sin\alpha =m.g.Sin\alpha$
$\displaystyle {{F}_{s}}=\mu {{N}^{'}}=\mu .G.Cos\alpha =\mu .m.g.Cos\alpha$
$\displaystyle \sum F=m.a=m.g.Sin\alpha -\mu .m.g.Cos\alpha$
$\displaystyle a=g\left( Sin\alpha -\mu .Cos\alpha \right)$ bulunur.

Bir sürtünmeli eğik düzlemde bir cisim sabit hızla aşağıya doğru hareket ediyorsa.
$\displaystyle \sum F={{F}_{x}}-{{F}_{s}}=0$ olup
$\displaystyle {{F}_{x}}={{F}_{s}}$
$\displaystyle m.g.Sin\alpha =\mu .m.g.Cos\alpha$
$\displaystyle \frac{Sin\alpha }{Cos\alpha }=\mu \Rightarrow Tan\alpha =\mu$

Atwood Aleti:

Tavana asılmış sabit bir makaradan geçen ipin uçlarına asılı m1 ve m2 kütlelerinden oluşan sistemdir.

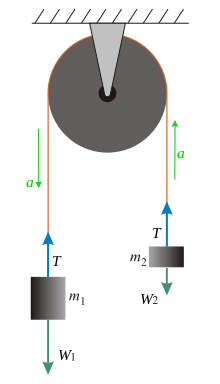
Sistemdeki iplerdeki T gerilme kuvvetleri eşit büyüklüktedir.
m1 ) m2 ise sistemi harekete geçiren net bileşke kuvvet

$\displaystyle \sum F={{G}_{1}}-{{G}_{2}}$
$\displaystyle \sum F={{m}_{1}}g-{{m}_{2}}g$
$\displaystyle \sum F=\left( {{m}_{1}}+{{m}_{2}} \right).a$
$\displaystyle \left( {{m}_{1}}+{{m}_{2}} \right).a=g.\left( {{m}_{1}}-{{m}_{2}} \right)$
$\displaystyle a=\frac{\left( {{m}_{1}}-{{m}_{2}} \right)}{\left( {{m}_{1}}+{{m}_{2}} \right)}.g$

İvmeli Referans Çerçevelerinde Hareket

Duran ya da sabit hızla hareket eden bir otobüsün tavanına asılı bir sarkaç, otobüs üzerine etki eden net bileşke kuvvet $\displaystyle \left( \sum F=0 \right)$ sıfır olduğu için denge konumunu koruyacağından düşey doğrultuda kalır.

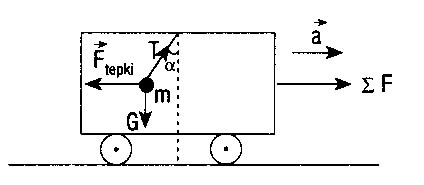
Otobüs a ivmesiyle sağa doğru hareket ediyorsa sarkaca ivmeli hareketten dolayı $\displaystyle \sum F=m.a$ etki kuvveti etkir. Newton’un III. Kanunu etki-tepki kanununa göre sarkaç Ftepki kuvvetinin etkisiyle düşey doğrultudan sola doğru (a) açısı kadar ayrılır.