Tam Değer Fonksiyonu Özellikleri, Örnekleri ile Birlikte Konu Anlatımı

Tam değer fonksiyonu nedir? Matematikte Tam değer fonksiyonu özelliklerinin örnekleri ile birlikte açıklanmaya çalışıldığı konu anlatımı.

TAM DEĞER FONKSİYONU

Tanım: x ∈ R için x’den büyük olmayan en büyük tamsayıya x’in tam değeri denir ve; $\displaystyle \left[\!\left[ x \right]\!\right]$ şeklinde gösterilir.

$\displaystyle \left[\!\left[ 2 \right]\!\right]=2$
$\displaystyle \left[\!\left[ 1,5 \right]\!\right]=1$
$\displaystyle \left[\!\left[ -3,5 \right]\!\right]=-4$
$\displaystyle \left[\!\left[ \sqrt{2} \right]\!\right]=1$

$\displaystyle \forall x\in R$ için, $\displaystyle \left[\!\left[ x \right]\!\right]\le x<\left[\!\left[ x \right]\!\right]+1$ dir.

$\displaystyle A\subset R$ olmak üzere, $\displaystyle f\left( x \right)=\left[\!\left[ x \right]\!\right]$ ile tanımlı $\displaystyle f:A\to R$ fonksiyonuna tam değer fonksiyonu denir.

ÖRNEK:

R’de $\displaystyle \left[\!\left[ 3x-1 \right]\!\right]=4$ denkleminin çözüm kümesi nedir?

$\displaystyle \left[\!\left[ 3x-1 \right]\!\right]=4\Rightarrow 4\le 3x-1<5$ olması gerekir.

$\displaystyle \Rightarrow 5\le 3x<6$
$\displaystyle \Rightarrow \frac{5}{3}\le x<2$

$\displaystyle C=\left[ 5/3,2 \right)$ olur.

ÖRNEK:

$\displaystyle f\left( x \right)=\frac{2}{\left[\!\left[ x \right]\!\right]-x}$ fonksiyonunun en geniş tanım kümesi nedir?
$\displaystyle \left[\!\left[ x \right]\!\right]-x=0$ olan ve x değerleri için fonksiyon tanımsızdır.

$\displaystyle \left[\!\left[ x \right]\!\right]-x=0\Rightarrow \left[\!\left[ x \right]\!\right]=x$ olup bu da x ∈ Z için geçerlidir. Bu sebepten dolayı en geniş çözüm kümesi T=R-Z olur.

ÖRNEK:

R’de $\displaystyle \left[\!\left[ 2x-5 \right]\!\right]\le 6$ eşitsizliğini çizelim.

$\displaystyle \left[\!\left[ 2x-5 \right]\!\right]\le 6\Rightarrow 2x-5<7$ olmalıdır.
$\displaystyle 2x-5<7\Rightarrow 2x<12\Rightarrow x<6$ olur.
$\displaystyle =\left( -\infty ,6 \right)$

ÖRNEK:

$\displaystyle \left[ -3,2 \right]\to R,f\left( x \right)=\left[\!\left[ x \right]\!\right]$ fonksiyonunun grafiğini çiziniz.
$\displaystyle -3\le x<-2\Rightarrow f\left( x \right)=-3$
$\displaystyle -2\le x<-1\Rightarrow f\left( x \right)=-2$
$\displaystyle -1\le x<0\Rightarrow f\left( x \right)=-1$
$\displaystyle 0\le x<1\Rightarrow f\left( x \right)=0$
$\displaystyle 1\le x<2\Rightarrow f\left( x \right)=1$
$\displaystyle x=2\Rightarrow f\left( x \right)=2$

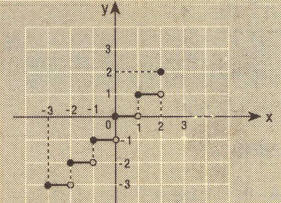
Tam Değer Fonksiyonu

Not: m ∈ Q olmak üzere $\displaystyle f\left( x \right)=\left[\!\left[ mx \right]\!\right]$ in grafiğini çizmek için her [a,a+1) aralığı;

$\displaystyle \left[ \frac{a}{m},\frac{a+1}{m} \right)$ alt aralıklarına bölünür. Bu durumda $\displaystyle \left[\!\left[ 2x \right]\!\right]$ in grafiğinde adım genişliği 1/2, $\displaystyle \left[\!\left[ \frac{x}{2} \right]\!\right]$ nin grafiğinde adım genişliği 2 olur.

$\displaystyle \left[ 4,16 \right)$ aralığında $\displaystyle y=\left[\!\left[ \sqrt{x} \right]\!\right]$ grafiği için adımlar 4,9,16 olur.

[0,3) aralığında $\displaystyle y=\left[\!\left[ {{x}^{2}} \right]\!\right]$ için adımlar 0,1, $\displaystyle \sqrt{2}$ , $\displaystyle \sqrt{3}$ olur.