Üçgen Eşliği

Üçgenlerin eşliği nedir? Üçgende benzerlik, açı-kenar-açı ve kenar-kenar-kenar eşlik teoremleri, açıklamaları.

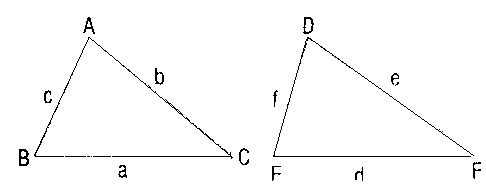
ucgende-eslik

ABC ile DEF üçgenleri arasında yapılan ABC ↔ DEF eşlemesinde karşılıklı kenarlar ve karşılıklı açılar eş ise, bu eşleme bir eşliktir.

$\displaystyle \overset{\Delta }{\mathop{ABC}}\,\cong \overset{\Delta }{\mathop{DEF}}\,$ biçiminde gösterilir.

Eşlik AKSİYOMU: KAK İkişer kenarı ile bu iki kenarın belirttiği açıları eş olan iki üçgen eştir.

$\displaystyle \left. \begin{array}{l}m\overset{\wedge }{\mathop{B}}\,=m\overset{\wedge }{\mathop{E}}\,\\a=d\\c=f\end{array} \right\}\Rightarrow \overset{\Delta }{\mathop{ABC}}\,\cong \overset{\Delta }{\mathop{DEF}}\,$

$\displaystyle m\overset{\wedge }{\mathop{B}}\,=m\overset{\wedge }{\mathop{E}}\,\Rightarrow \overset{\Delta }{\mathop{ABC}}\,\cong \overset{\Delta }{\mathop{DEF}}\,$

(AKA) EŞLİK TEOREMİ

İki üçgenin ikişer açıları ile bu açıların köşelerini birleştiren kenarları karşılıklı olarak eş ise, bu iki üçgen eştir.

$\displaystyle \left. \begin{array}{l}m\overset{\wedge }{\mathop{B}}\,=m\overset{\wedge }{\mathop{E}}\,\\a=d\\m\overset{\wedge }{\mathop{C}}\,=m\overset{\wedge }{\mathop{F}}\,\end{array} \right\}\Rightarrow \overset{\Delta }{\mathop{ABC}}\,\cong \overset{\Delta }{\mathop{DEF}}\,$

(K.K.K) EŞLİK TEOREMİ

İki üçgenin karşılıklı üçer kenarı eş ise, bu iki üçgen eştir.

$\displaystyle \left. \begin{array}{l}a=d\\b=e\\c=f\end{array} \right\}\Rightarrow \overset{\Delta }{\mathop{ABC}}\,\cong \overset{\Delta }{\mathop{DEF}}\,$