Advertisement
Üçgenlerde açıların özellikleri nelerdir? Maddeler halinde açıklamalı, üçgende açılar ile ilgili özellikler, formüller.
Üçgende Açılarla İlgili Özellikler
a) Üçgende açıların toplamı
Üçgenin iç açılarının toplamı 180, dış açılarının toplamı 360’dır.
b) İki iç açıortayın belirttiği açı
Advertisement
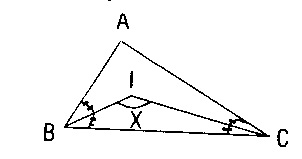
ABC de B ve C açıortaylarının kesim noktası I ise,
c) İki dış açıortayın belirttiği açı:
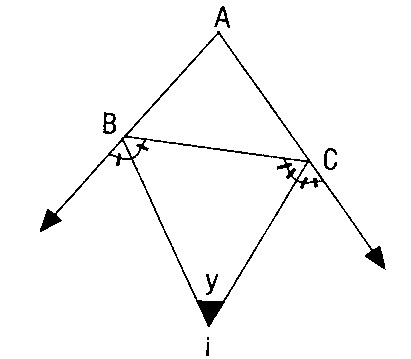
ABC üçgeninde B ve C açılarının dış açı ortaylarının kesim noktası J ise
Advertisement
d-Bir iç ve bir dış açıortayın belirttiği açı:
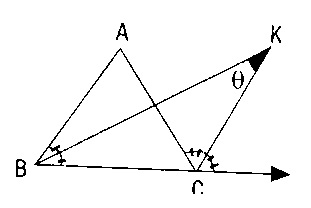
ABC de B nin iç açıortayı ile C nin dış açıortayının kesim noktası K ise
e) 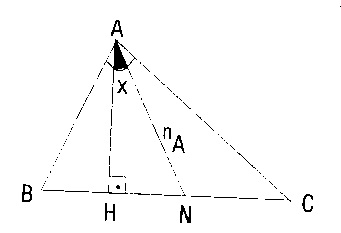
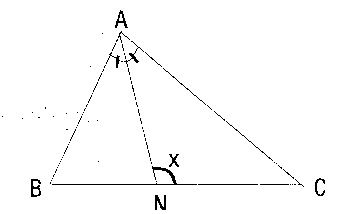
ABC üçgeninde [AH] yüksekliği ile [AN] açıortayının belirttiği açının ölçüsü
f -Bir üçgende iki köşeye ait yüksekliklerin arasında kalan açının ölçüsü, bu köşelerdeki iç açıların ölçüleri toplamına eşittir.
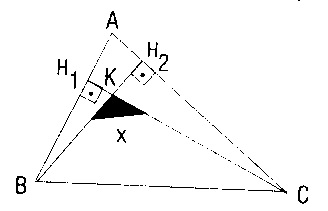
g) 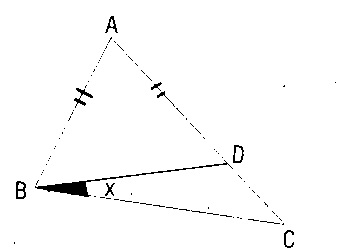
Advertisement
h) 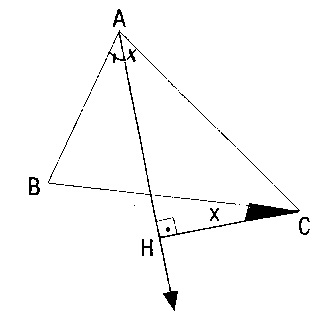
şekilde [AH], A açısının açıortayıdır.
i) AN açıortay ise,