Üçgende Kenarortay Bağıntıları

0

By gurur on 22 Eylül 2014 Bilgi Dünyası

Advertisement

Üçgende kenarortay nedir? Üçgende kenarortay bağıntıları, özellikleri, denklemleri ve formüller.

Üçgende Kenarortay Bağıntıları

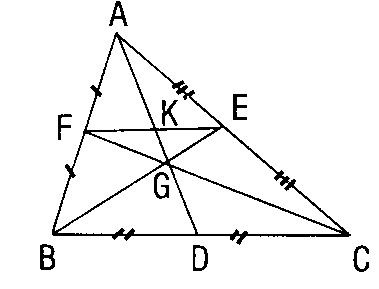
ucgende-kenarortay

Bir üçgende kenarların orta noktasını karşı köşelere birleştiren doğru parçalarına üçgenin kenar ortayları denir. |AD| = V_a, |BE| = V_b |CF| = V_c biçiminde gösterilir.

Bir üçgende üç kenar ortay bir noktada kesişir. Bu noktaya üçgenin ağırlık merkezi denir.

Ağırlık merkezinin kenara uzaklığı 1 birim ise köşeye uzaklığı 2 birimdir.

Advertisement

$\displaystyle \left| GD \right|=x\Rightarrow \left| GA \right|=2x$

$\displaystyle \left| GD \right|=x\Rightarrow \left| AD \right|=3x$

$\displaystyle \left| AG \right|=\frac{2}{3}{{V}_{a}}$

$\displaystyle \left| GD \right|=\frac{1}{3}{{V}_{a}}$

$\displaystyle \left| BG \right|=\frac{2}{3}{{V}_{b}}$

$\displaystyle \left| GE \right|=\frac{1}{3}{{V}_{b}}$

Advertisement

$\displaystyle \left| GC \right|=\frac{2}{3}{{V}_{c}}$

$\displaystyle \left| GF \right|=\frac{1}{3}{{V}_{c}}$

$\displaystyle \left| KG \right|=\frac{1}{6}{{V}_{a}}$

$\displaystyle \left[ FE \right]\parallel \left[ BC \right]$

$\displaystyle \left| FE \right|=\frac{\left| BC \right|}{2}$

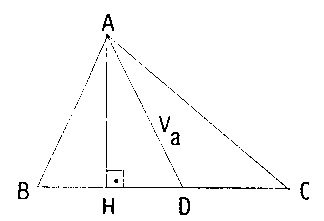
ucgende-kenarortay-1

Şekilde AH Yükseklik D kenarortay

$\displaystyle \left| HD \right|=x\Rightarrow \left| BD \right|=\left| DC \right|=\frac{a}{2}$

$\displaystyle {{b}^{2}}+{{c}^{2}}=2V_{a}^{2}+\frac{{{a}^{2}}}{2}$

$\displaystyle {{b}^{2}}-{{c}^{2}}=2ax$

$\displaystyle m\overset{\wedge }{\mathop{A}}\,<90{}^\circ \Rightarrow {{V}_{a}}>\frac{a}{2}$

Advertisement

$\displaystyle m\overset{\wedge }{\mathop{A}}\,=90{}^\circ \Leftrightarrow {{V}_{a}}=\frac{a}{2};5V_{a}^{2}=V_{b}^{2}+V_{c}^{2}$

$\displaystyle m\overset{\wedge }{\mathop{A}}\,>90{}^\circ \Rightarrow {{V}_{a}}<\frac{a}{2}$

Leave A Reply Cancel Reply