Üçgende Kenarortay Teoremi

Üçgende kenarortay teoremleri, formülleri. Üçgenlerin kenarortay teoremlerinin açıklaması, ve formülü.

KENARORTAY TEOREMLERİ

1. Bir üçgende iki kenarın uzunluklarının kareleri toplamı, üçüncü kenarın uzunluğunun karesinin yarısı ile bu kenara ait kenar ortay uzunluğunun karesinin iki katı toplamına eşittir.

Bir $\displaystyle \overset{\Delta }{\mathop ABC}\,$ de kenarlar a, b, c, ve bu kenarlara ait kenarortaylar sırası ile Va,Vb,Vc ise

$\displaystyle {{b}^{2}}+{{c}^{2}}=\frac{{{a}^{2}}}{2}+2V_{a}^{2}\Rightarrow$

$\displaystyle {{V}_{a}}=\frac{1}{2}\sqrt{2{{b}^{2}}+2{{c}^{2}}-{{a}^{2}}}$

$\displaystyle {{a}^{2}}+{{c}^{2}}=\frac{{{b}^{2}}}{2}+2V_{b}^{2}\Rightarrow$

$\displaystyle {{V}_{b}}=\frac{1}{2}\sqrt{2{{a}^{2}}+2{{c}^{2}}-{{b}^{2}}}$

$\displaystyle {{a}^{2}}+{{b}^{2}}=\frac{{{c}^{2}}}{2}+2V_{c}^{2}\Rightarrow$

$\displaystyle {{V}_{c}}=\frac{1}{2}\sqrt{2{{a}^{2}}+2{{b}^{2}}-{{c}^{2}}}$

Bir $\displaystyle \overset{\Delta }{\mathop ABC}\,$ de

$\displaystyle 4\left( V_{a}^{2}+V_{b}^{2}+V_{c}^{2} \right)=3\left( {{a}^{2}}+{{b}^{2}}+{{c}^{2}} \right)$

bağıntısı vardır.

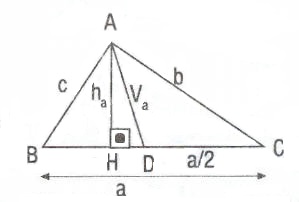
kenarortay-teoremi

Bir üçgende iki kenarın uzunluklarının kareleri farkı, üçüncü kenarının uzunluğunun iki katı ile üçüncü kenara ait kenarortayın üçüncü kenar üzerindeki izdüşümünün uzunluğu çarpımına eşittir. Yukarıdaki şekilde [HD], V_a nın a kenarı üzerindeki dik izdüşümüdür. $\displaystyle \left| HD \right|=x$ ise $\displaystyle \left| {{b}^{2}}-{{c}^{2}} \right|=2ax$ dir.