Uzayda Düzlemin Vektörel Denklemi

12. sınıf geometri konusu, Uzayda Düzlemin Vektörel Denklemi nedir, nasıl hesaplanır, örnek sorular.

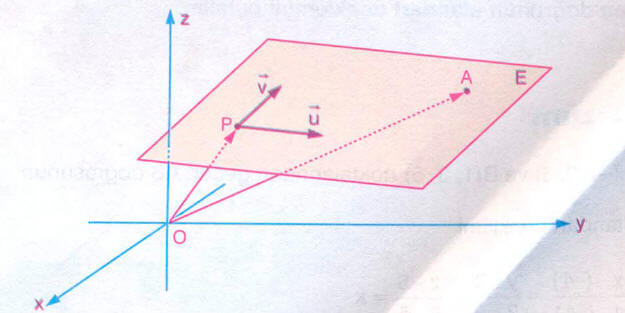
Uzayda Düzlemin Vektörel Denklemi

Uzayda,

bir P noktasından geçen ve lineer bağımsız u ve v vektörlerine paralel olan düzlemin vektörel denklemi,

olur.

A noktası düzlem üzerinde değişken bir nokta ve k1, k2 ∈ R dir.

k1, k2 ye düzlemin parametreleri,

u ve v ye düzlemin doğrultu vektörleri denir.

Örnek:

Analitik uzayda, P(3, 2, 5) noktasından geçen bir düzlem u = (1, 2, -1) ve v = (-2, 3, 2) vektörlerine paraleldir.

Buna göre, bu düzlemin vektörel denklemini bulalım.

Çözüm:

A(x, y, z) düzlem üzerinde herhangi bir nokta olmak üzere

(x, y, z) = (3, 2, 5) + k(1,2,-1) + n(-2, 3, 2) (n, k ∈ R) bulunur.

Örnek:

Vektörel denklemi,

(x, y, z) = (-4, 6, 1) + k(-2, 3, 2) + n(3, 4, 1) (n, k ∈ R) olan bir düzlem veriliyor.

Buna göre, düzlem üzerinde k = 3 ve n = -2 değerlerinin belirttiği noktanın koordinatlarını bulalım.

Çözüm:

k = 3 ve n = -2 değerlerinin belirttiği nokta A olsun.

A(x, y, z) = (-4, 6, 1) + 3 . (-2, 3, 2) + (-2) . (3, 4, 1)

A(x, y, z) = (-4, 6, 1) + (-6, 9, 6) + (-6, -8, -2)

A(x, y, z) = (-16, 7, 5) bulunur.

NOT:

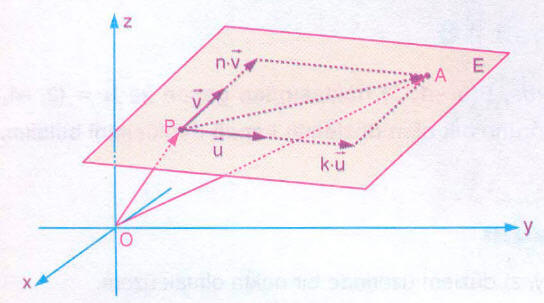
P, E düzlemi üzerinde bir nokta, ve doğrultu vektörleri olmak üzere,

düzlem üzerindeki her bir A noktası için,

vektörünü; ,  ve vektörlerinin lineer bileşimi olarak yazacak şekilde k ve n sayıları bulunabilir.

Yukarıdaki şekilde de görüldüğü gibi,

Bu eşitlik düzlemin vektörel denklemidir.

Burada, biçiminde de yazılabilir.