12. sınıf geometri dersi uzayda vektör konusu anlatımı. Vektör özellikleri, vektörde işlemler, toplama, çıkarma, çarpma kısa özeti.
Uzayda Vektör
Yönlü doğru parçalan üzerinde tanımlanan denklik (~) bağıntısına göre, doğrultuları ve yönleri aynı, uzunlukları eşit olan yönlü doğru parçaları aynı denklik sınıfında bulunur.
ve
nin doğrultu ve yönleri aynı, uzunlukları eşittir.
Tanım
Yönlü doğru parçaları üzerinde tanımlanan ~ (denklik, eşlik) bağıntısının her bir denklik sınıfı bir vektördür.
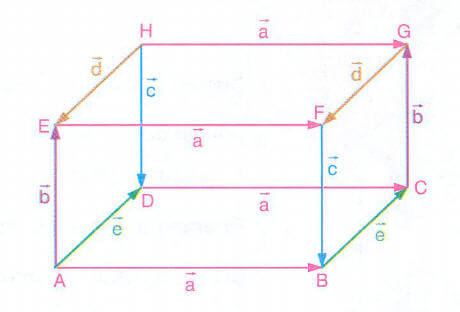
Şekildeki dikdörtgenler prizması üzerinde doğrultu ve yönleri aynı, uzunlukları eşit olan yönlü doğru parçaları aynı denklik sınıfında bulunur ve her bir denklik sınıfı bir vektördür. Yukarıdaki şekilde verilenlere göre,
olur.
Uzayda, bir A noktası ve bir vektörü verildiğinde,
olacak şekilde bir tek B noktası vardır.
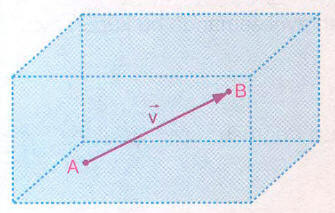
Şekildeki uzay modelinde, vektörünün başlangıç noktası A, bitiş noktası B dir.
Uzayda, A ve B noktası verildiğinde, olacak şekilde bir tek
vektörü vardır.
Tanım
Uzunluğu 1 birim olan vektöre birim vektör denir. Başlangıç ve bitimi aynı olan yönlü doğru parçalarının denklik sınıfına sıfır vektörü denir. Sıfır vektörü veya
diye gösterilir.
Örnek:
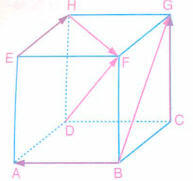
Küpün kenarları 1 birim olduğundan, şekildeki vektörleri birim vektördür.
Vektörler Kümesinde İşlemler
Uzaydaki bütün vektörler kümesi V ile gösterilir.
Uzayda vektörlerde toplama, çıkarma, eksi ile çarpma veya skalerle çarpma işlemleri ve özellikleri düzlemdeki işlemlere benzerdir.
a. Vektörlerde Toplama
Uzayda vektörlerde toplama işlemi uç uca ekleme yöntemi ile yapılabilir.
Örnek:
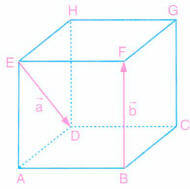
Şekildeki küpte, ve
vektörleri veriliyor.
Buna göre, toplam vektörünü bulalım.
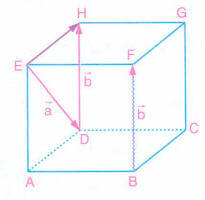
vektörünü, başlangıç noktası
vektörünün bitiş noktasına gelecek şekilde taşıyalım.
Bu durumda, vektörünün başlangıç noktasını
vektörünün bitiş noktasına birleştiren
vektörü toplam vektörüdür.
b. Vektörlerde Çıkarma
Doğrultuları ve uzunlukları aynı, yönleri farklı olan ve
vektörleri için
dir.
Uzaydaki ve
vektörleri için,
diye gösterilir.
Örnek:
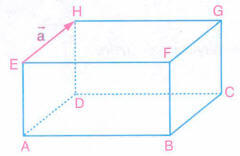
Şekildeki dikdörtgenler prizmasında, veriliyor.
olduğuna göre, başlangıç ve bitiş noktaları prizmanın köşeleri olan ve
vektörüne eş olan vektörleri bulalım.
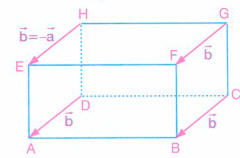
vektörü,
ile aynı doğrultuda, eşit uzunlukta fakat farklı yönlerdedir.
Buna göre, olur.
c- Vektörlerde Skalerle Çarpma
Uzayda, bir vektör ve k bir reel sayı olmak üzere,
k • vektörü,
k > 1 ise,
aynı yön ve doğrultuda vektöründen daha uzun bir vektör,
0 < k < 1 ise,
aynı yön ve doğrultuda vektöründen daha kısa bir vektör,
-1 < k < 0 ise,
aynı doğrultuda, farklı yönde vektöründen daha kısa bir vektör,
k < -1 ise,
aynı doğrultuda, farklı yönde vektöründen daha uzun bir vektör olur.
Örnek:
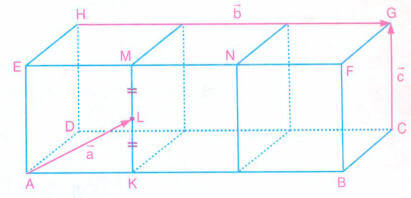
Yukarıdaki şekil üç tane birim küpün birleşimiyle oluşmuştur. ,
ve
veriliyor.
|KL| = |LM| olduğuna göre, vektörünü bulalım.
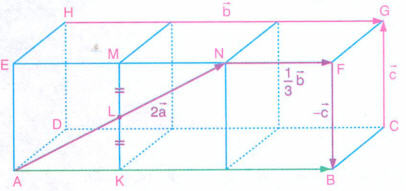
Şekle göre, vektörü olur.