Vektörel işlemler fizik 10. sınıf konusu, vektörlerin toplanması, çıkarılması, skalerle çarpılması konu anlatımı, örnekler.
VEKTÖREL İŞLEMLER
Vektörlerin Toplanması (Bileşke vektör)
a) Paralelkenar yöntemi
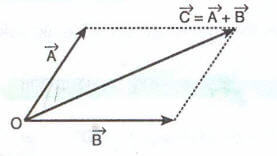
Başlangıç noktaları birleştirilen iki vektör paralel kenara tamamlanırsa paralel kenarın “O” başlangıç noktasından geçen köşegeni toplam vektördür.
b) Çokgen (uç uca ekleme) yöntemi
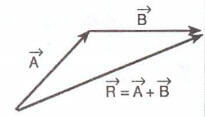
Vektörlerin birinin bitim noktası ile diğerinin başlangıç noktası çakıştırılır. İlk vektörün başlangıç noktası ile son vektörünün bitim noktası birleştirilirse elde edilen vektör toplam vektörü verir.
c) Dik bileşenlere ayırma yöntemi
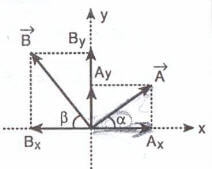
Vektörler dik koordinat sistemi üzerindeki bileşenlerine ayrıldıktan sonra, x ve y eksenlerinde toplamları alınarak iki dik vektöre dönüştürülür.
ve
vektörlerinin bileşkesi
ise,
VEKTÖRLERİN ÇIKARILMASI
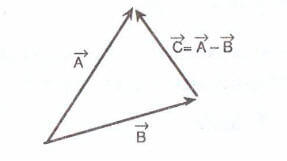
- a) Önünde (-) işareti olan vektör ters çevrilerek, toplama kuralları uygulanabilir.
- b) Vektörlerin başlangıç noktaları birleştirilip (-) vektör ucundan (+) vektör ucuna çizilen vektör fark vektörüdür.
VEKTÖRLERİN SKALERLE ÇARPILMASI
Bir vektörün bir skalerle çarpımı veya bölümü bir vektör verir.
- a) Skaler pozitif ise elde edilen vektör esas vektörle aynı yönlüdür.
- b) Skaler negatif ise elde edilen esas vektör ile zıt yönlüdür.
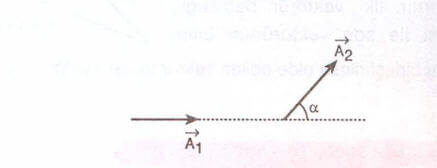
ve
vektörlerinin bileşkesinin şiddeti,
bağıntısından hesaplanır.
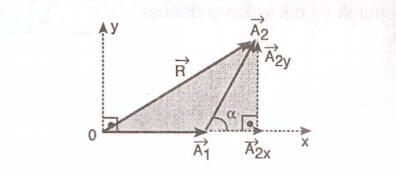
A1 vektörünün ucuna A2 vektörü taşınır. A2 vektörü birbirine dik A2x ve A2y bileşenlerine ayrılır. Taralı üçgenin hipotenüsü bileşke vektörü verir.
(Kosinüs Teoremi)
- ***İki vektörün bileşkesinin şiddeti, iki vektörün toplamından büyük farkından küçük olamaz.
- ***Büyüklükleri farklı iki vektörün bileşkesi büyük olan bileşenle daha küçük açı yapar.
- ****İki vektör arasındaki açı küçüldükçe bileşkenin büyüklüğü artar.
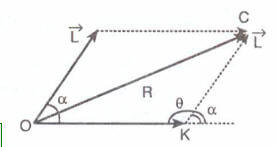
Şekilde görüldüğü gibi iki vektör arasındaki α açısı küçüldükçe ‘ninde R’nin karşısısındaki Θ açısı büyür. Dolayısıyla bileşke vektör
büyür.
Skaler ve Vektörel Büyüklükler
Fizikte iki tür büyüklük vardır.
Skaler büyüklük: Sayı ve birimi ile tanımlanabilen büyüklüklerdir. Bu nedenle sadece sayısal değeri olan büyüklüklerdir.
Vektörel büyüklük: Sayı, birimi, yönü ve doğrultusu ile tanımlanabilen büyüklüklere denir.
Bir vektörün tanımlı olabilmesi için,
- – Uygulama noktası
- – Yönü ve doğrultusu
- – Büyüklüğü tanımlanmış olmalıdır.
Vektörlerin özellikleri
- * Doğrultu ve yönü değiştirilmeden bir vektör istenilen yere taşınabilir.
- * iki vektörün eşit olabilmesi için doğrultusu, yönü ve büyüklüğü aynı olmalıdır.
- * Büyüklük ve doğrultusu aynı, yönü ters olan iki vektöre zıt vektörler denir. Başka bir deyişle toplamları sıfır olan vektörlere zıt vektörler denir.
- * Bir vektörün büyüklüğü; yönünden bağımsız, her zaman pozitiftir.