Yüklü parçacıkların ivme hızları, yönleri nereye doğrudur? Yüklü parçacıkların ivme ve hız hesaplaması, formülleri hakkında bilgi.
YÜKLÜ PARÇACIKLARIN İVME VE HIZLARI
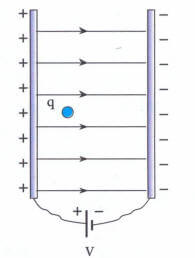
Paralel levhalar arasındaki düzgün bir elektrik alanı içinde ağırlığı ihmal edilen yüklü parçacık bırakılınca sabit F elektriksel kuvvetin etkisiyle sabit ivmeli hareket yapar, ivmenin büyüklüğü dinamiğin temel prensibinden,
şeklinde bulunur.
Parçacığın ivmesi, yükü ve levhalar arasındaki potansiyel farkı ile doğru kütlesi ve levhalar arasındaki uzaklıkla ters orantılıdır. îvme vektörünün yönü ise, elektriksel kuvvetin yönündedir.
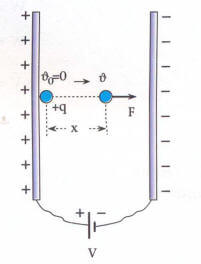
Şekildeki gibi +q yüklü parçacık hızıyla karşı levhaya doğru elektrik alan doğrultusunda atılmaktadır. Bu parçacığın hareketi incelenecek olursa:
Parçacık +q yüküne sahip ise, parçacığa etkiyen sabit kuvvet elektrik alan yönünde olacağından düzgün hızlanan hareket yaparak t saniye sonra karşı levhaya hızıyla çarpar. Karşı levhaya dik olarak çarpması parçacığın ağırlığının ihmal edildiğini belirtir.
1) Eğer parçacığın ilk hızı sıfır ise, harekete başladıktan t süre sonra hızı,
ve bu sürede aldığı yol;
olur.
Elektrik alan içinde serbest bırakılan yüklü parçacık bir noktadan başka bir noktaya hareketi sonunda elektrik alandan enerji alır ve kinetik enerji kazanır. Elektrik alanda yapılan iş,
olur, bu da cismin kazandığı kinetik enerjiye eşittir. Buna göre,
olur.
(+) levhadan serbest bırakılan yüklü cisim, (-) levhaya ulaştığında kinetik enerjisi,
olur.
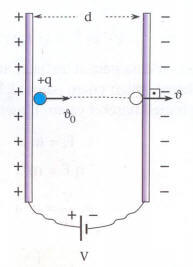
2) Şekilde görüldüğü gibi ilk hızı olan parçacığın karşı levhaya çarpma hızı iki yoldan bulunabilir:
a) Zamansız hız formülünden
olarak bulunur.
Burada çarpma hızının, levhalar arası d uzaklığına bağlı olmadığı görülmektedir.
b) Parçacık üzerinde levhalar arasında yapılan iş, parçacığın kinetik enerjisindeki değişme miktarına eşittir.
ifadesi bulunur. Görüldüğü gibi bu sonuç önceki bulunan sonuçla aynıdır.
3) Parçacık düzgün hızlanan doğrusal hareket yaptığından karşı levhaya çarpma süresi,
denkleminden ya da denkleminden bulunur.
İvmenin değerinin olduğu unutulmamalıdır.
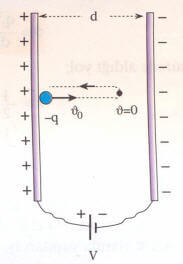
4) Parçacık -q yüküne sahipse, parçacığa etkiyen kuvvet elektrik alanına zıt yönde olacaktır. Bu da ilk hareket yönüne terstir.O halde parçacık düzgün yavaşlayan hareket yapacaktır. Verilen değerlere göre, parçacık karşı levhaya çarpabilir ya da çarpmayabilir.
Çarpmıyorsa, yavaşlayarak levhalar arasında x kadar yol alarak durur ve tekrar ters yönde düzgün hızlanan hareket yapar. Sorulan nicelikleri bu hareketin özelliklerinden bulabiliriz.
Parçacığın atıldığı andaki kinetik enerji ile, harekete ters yönde yapılan iş değerleri karşılaştırıldığında,
- a)
ise, parçacık karşı levhaya çarpar.
- b)
ise, karşı levhaya çarpma anında durur ve geri dönerek hızlanır.
- c)
ise, karşı levhaya ulaşamadan durur ve geriye doğru tekrar hızlanır.