Yuvarlanma Hareketi Konu Anlatımı

Yuvarlanma Hareketi nedir? Yuvarlanma hareketinin özellikleri, formülleri, örnekli konu anlatımı, Yuvarlanma Hareketi hakkında bilgi.

Yuvarlanma Hareketi Konu Anlatımı

yuvarlanma hareketi

YUVARLANMA HAREKETİ NEDİR? ÖZELLİKLERİ NELERDİR?

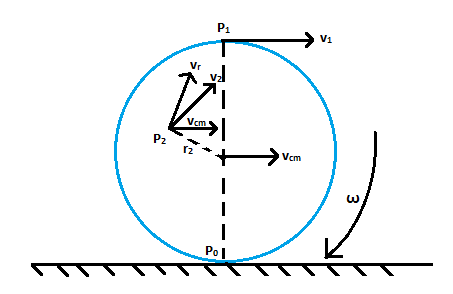
Aşağıdaki şekildeki gibi yuvarlanan bir çemberi gözönüne alalım. Çember, kütle merkezi çevresinde ω açısal hızıyla dönüyor olsun. Tam bir devir yaptığında da kütle merkezi,

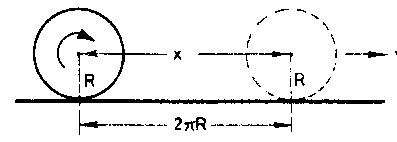
yuvarlanan-cember

$\displaystyle x=2\pi R$

yolunu alır. Bu sırada çember üzerindeki bir nokta ise 2 π radyanlık açı dönmüş olacağından

$\displaystyle \omega =\frac{2\pi }{T}$

kütle merkezinin öteleme hızı,

$\displaystyle v=\frac{x}{T}=\frac{2\pi R}{T}=\omega R$

olur. Demek ki kütle merkezinin ilerleme hızıyla çember üzerindeki bir noktanın çizgisel hızı eşit olmaktadır. Yuvarlanan bir cismin herhangi bir noktasının anlık hızı bu iki hızın bileşkesi olur. Dönme hareketinin çizgisel hızı v_D, öteleme hareketinin hızı v_Ö ise, herhangibir noktanın anlık hızı,

$\displaystyle \overrightarrow{v}=\overrightarrow{{{v}_{D}}}+\overrightarrow{{{v}_{\ddot{O}}}}$ olur.

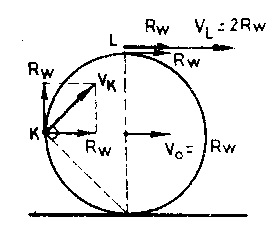
cemberin-anlik-hizlari

Örneğin Yukarıdaki çemberin K ve L noktalarının anlık hızları,

$\displaystyle v_{K}^{2}=v_{D}^{2}+v_{\ddot{O}}^{2}={{\left( R\omega \right)}^{2}}+{{\left( R\omega \right)}^{2}}$

$\displaystyle {{v}_{K}}=R\omega \sqrt{2}$

$\displaystyle {{v}_{L}}=R\omega +R\omega =2R\omega$ olur.

cember-yuvarlanmasi

Görülüyor ki, çember üzerindeki K ve L noktalarının dönüş çizgisel hızları eşit olduğu halde anlık v_K ve v_L hızları farklı değerde ve v_L> v_K olmaktadır. Ayrıca v_K vektörüne K noktasından çizilen dikme ile v_L vektörüne L noktasından çizilen dikme, çemberin yere değme noktasından geçmektedir. Bu noktaya yuvarlanma hareketinin anlık ekseni denir. Bir yuvarlanma hareketi, daima, anlık eksen çevresinde aynı açısal hızla yapılan bir dönme hareketine eşdeğerdir. Yani çember yuvarlanırken K noktası, D noktası çevresinde r_K yarıçaplı çember üzerinde v_K hızıyla dönüyormuş gibi olur. Aynı şekilde L noktası da r_L = 2R yarıçaplı çember üzerinde v_L hızıyla döner. K ve L’nin bu dönüşlerinin açısal hızları aynı ve kütle merkezi çevresindeki dönüşün açısal hızına eşittir.