İki kesrin arasında bulunan kesirler nasıl bulunur? Kolay yollar ile kesirleri sıralama, aralarındaki kesirleri bulma.

İki Kesir Arasındaki Kesir
Kesir, iki bölümden oluşan bir değerdir; her kısım, pay veya payda bir tam sayıdır. Pay, kesirin üstteki sayısıdır, payda ise alttaki sayısıdır. Kesirlerde toplama ve çıkarma işlemleri yapabilmek için, ilgili kesirlerin paydalarının aynı değerde olmasını gerekir. İki kesir arasında bulunan kesirleri bulmak için ise, kesirli matematiği bırakıp daha basit bir yol izleyebiliriz.
Başlangıç Kesirlerini Yazın
Örnekle anlamak için iki kesir elde edin. Bizim örneğimizdeki kesirler;
ve
Payları Toplayın
Kesirlerin paylarını toplayın. Bu örnekte,
1 + 3 = 4
Paydaları Toplayın
Kesrin paydalarını toplayın. Bu örnekte,
2 + 4 = 6
Yeni Bir Kesir Yazın
Yeni pay olarak payların toplamı ve yeni payda olarak paydaların toplamı ile yeni bir kesir yazın. Bu örnekte, yeni kesir
Kesiri Sadeleştirin
Pay ve payda tarafından paylaşılan en büyük ortak faktörü ortadan kaldırarak kesri basitleştirin. Bunu yapmak için, her sayının çarpanlarını listeleyin ve en büyük paylaşılan sayıyı dışarıda bırakın.
Bu durumda, 4’ün çarpanları 1, 2 ve 4’tür ve 6’nın çarpanları 1, 2, 3 ve 6’dır. Her iki sayı da faktör olarak 1 ve 2’ye sahiptir ve 2 en büyük faktördür.
Hem paydan hem de paydadan 2’yi çıkarınca sonuç;
İpuçları
Cevabınızı kontrol etmek için, ortak paydaları olan kesirleri yazın ve payları karşılaştırın. Ortak paydalı 1/2, 2/3 ve 3/4 örnek kesirleri 6/12, 8/12 ve 9/12 olur. 8 payı 6 ile 9 arasındadır, bu nedenle oluşturduğunuz kesir – 8/12 veya basitleştirildiğinde 2/3 – başladığınız iki kesir arasındadır.
RASYONEL SAYILAR (KESİRLER)
Pay ve payda gibi iki sayının birbirine oranı şeklinde gösterilen ifadelere rasyonel sayı, kesir denir.
matematiksel ifadesi bir rasyonel sayıdır.
şeklinde adlandırılır.
a değeri bir tam sayıya karşılık gelmeli ve b değeri sıfır dışındaki herhangi bir tam sayı değeri olmalıdır.
ifadesinde payda sıfırdır ve bu ifade tanımsızdır.
gibi ifadeler (kesir) rasyonel sayıdır.
A. Kesirlerde Dört İşlem
Rasyonel sayılarda yapılacak matematiksel işlemler, sayılar konusunda yapılan matematiksel işlemlerle benzerlikler gösterir. Sayılar konusunda bütün sayıların paydaları 1 olduğundan toplama ve çıkarma işlemleri daha kolay yapılmaktaydı.
1. Toplama ve Çıkarma İşlemleri
Kesirlerde toplama ve çıkarma işlemi yaparken paydalar eşitse paylar toplanır payda ise olduğu gibi kalır.
Örneğin;
Rasyonel ifadelerin paydaları eşit değilse toplama işlemi yapmadan önce paydaların eşitlenmesi gerekir. Paydaları eşitlemek için bir rasyonel ifadenin pay ve payda değerleri aynı ifadelerle çarpılıp paylar toplanarak iki rasyonel ifadenin paydaları eşitlenmeye çalışılır. Bu eşitleme işlemleri pratik yaparak gelişecektir.
Rasyonel ifadelerde paydaların eşitlenmesi için rasyonel ifadenin payı ve paydası aynı sayıyla çarpılır.
Örneğin:
Rasyonel sayılarda toplama ve çıkarma işleminde ortak payda terimlere dağıtılabilir.
Örneğin:
2. Çarpma İşlemi
Rasyonel ifadelerde çarpma işlemi yaparken, toplama-çıkarma işlemlerinde olduğu gibi payda eşitlemeye gerek yoktur. Rasyonel ifadelerdeki paylar kendi arasında çarpılır ve sonuç pay olur, paydalar kendi arasında çarpılır ve sonuç payda olur.
Örneğin;
3. Bölme İşlemi
Bölme, çarpma işlemiyle benzer bir işlemdir. İki rasyonel ifade arasında bölme işlemi varsa birinci rasyonel ifade aynen yazılır, ikinci rasyonel ifade ters çevrilerek çarpma işlemi yapılır. Ulaşılan sonuç bu iki rasyonel ifadenin bölümüdür.
Örneğin;
Sayılar bölümünde işlem sırasıyla ilgili öğrendiğimiz bilgiler rasyonel ifadeler için de geçerlidir.
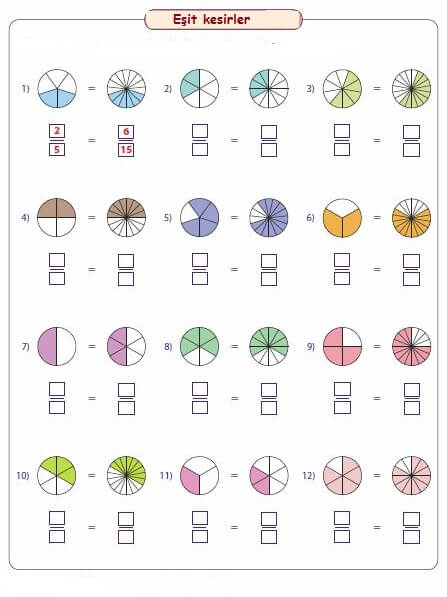
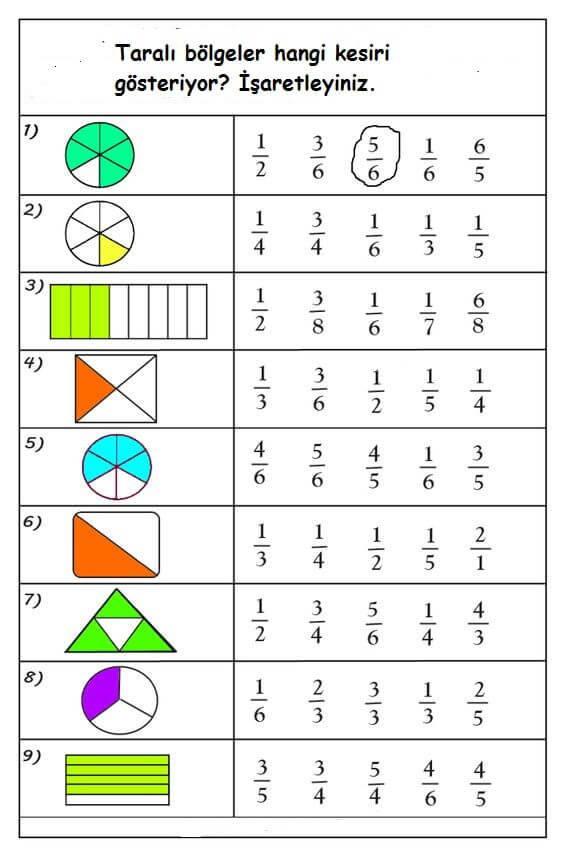
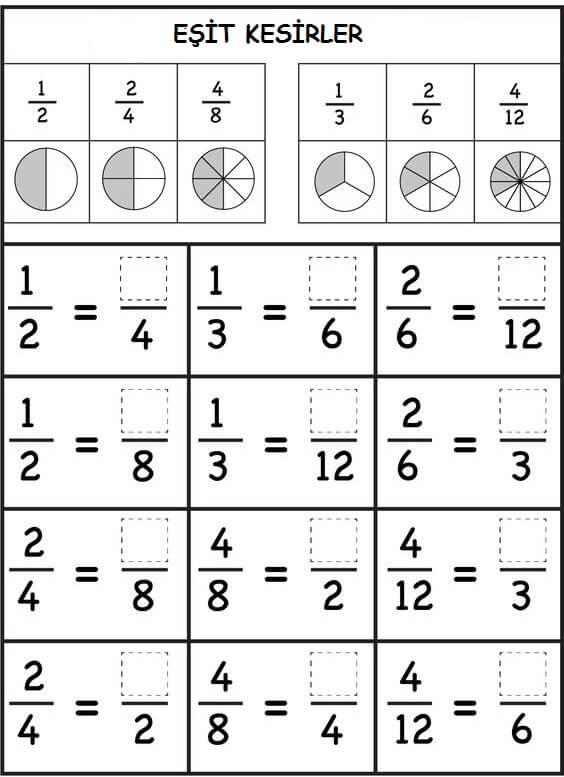
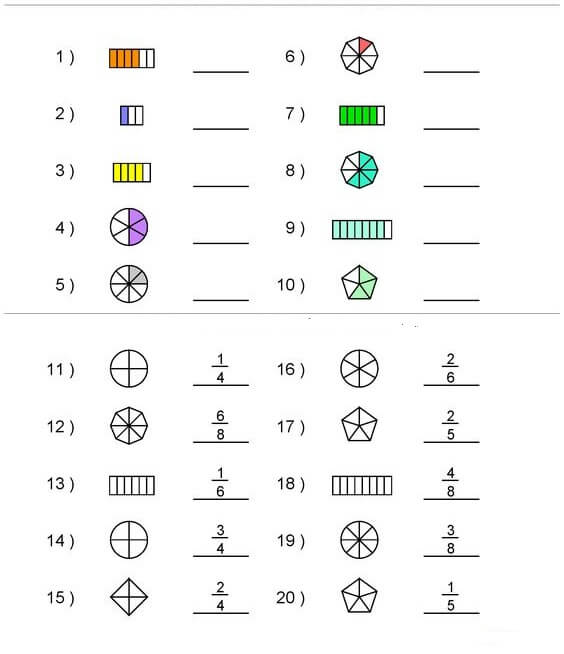
Kesirler İle İlgili Alıştırmalar