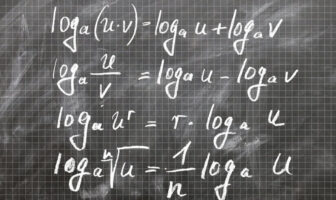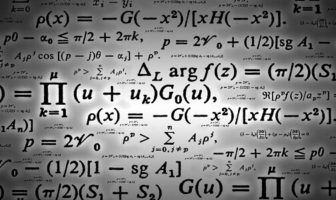A harfiyle başlayan matematik terimlerinin anlamlarını merak ediyor musunuz? Açıklık nedir, asal sayıların özellikleri nelerdir?…

1 kilo salça elde etmek için kaç kilo domatese ihtiyaç duyulur? Salça yapım süreci, domatesin…

1 den 10’a kadar olan sayıların küpleri ve kare üsleri nelerdir? Küp ve üs kavramlarına…

Merak edilen soruya cevap: 1’den 10’a kadar olan sayılara kalansız bölünebilen en küçük pozitif tam…

3. sınıf matematik için zihinden çıkarma işlemi nasıl yapılır? Adım adım anlatım, ipuçları ve örneklerle…

Okula yardımcı F Harfiyle başlayan matematik terimleri. F Harfi ile başlayan Matematik terimlerinin anlamları, açıklamaları, sözlüğü.…

Yüzyıl kavramını nasıl hesaplayacağınızı merak ediyor musunuz? Bu rehberde, yüzyıl hesaplama yöntemleriyle birlikte yarım ve…

Permütasyon ve Kombinezon nedir? Permütasyon ve Kombinezon hesaplamaları ve konuları ile ilgili olarak genel bilgilerin yer aldığı sayfamız. Permütasyon ve Kombinezon (Kombinasyon) Hesaplamaları Nasıl Olur? Permütasyon ve kombinezon, verili bir kümenin sıra gözetilerek (permütasyon) ya da gözetilmeksizin (kombinezon) seçilen öğelerinden oluşturulan farklı altkümeler. Permütasyon ve kombinezon kuramındaki gelişmeler ve verili bir durum için olanaklı permütasyon

Fields Madalyası nedir? Matematiğin Nobel’i olarak bilinen bu prestijli ödülün tarihini, kriterlerini, yaş sınırını, simgesel…

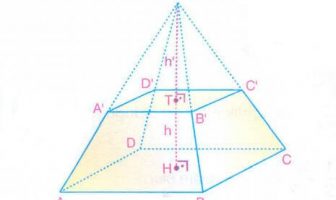
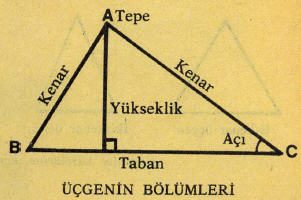
Matematiğin bir dalı olan ve hemen hemen tüm hesap işleri gerektiren bilim dallarının kullanmış olduğu trigonometri ile ilgili genel bilgilerin kısaca verildiği yazımız. Trigonometri, matematiğin önemli bir dalıdır ve açıların bazı büyüklükleri arasındaki bağıntıları inceler. Bu bilim dalı, açıların ve üçgenlerin incelenmesi üzerine odaklanır ve özellikle geometri ile yakından ilişkilidir. Trigonometrinin temel amacı, çeşitli açıların

Bileşke fonksiyon nedir? Bileşke fonksiyon nasıl çözülür? Bileşke fonksiyon konusu örneklerle anlatımı, soru ve çözümleri. BİLEŞKE FONKSİYON: f:A→B ve g:B→C fonksiyonları verilsin. f(x) = y ve g(y) = z olsun gof: A→C , (gof) (x) = z olan fonksiyona f ile g nin bileşke fonksiyonu denir. (gof) (x) = g[f(x)] dir. ÖRNEK: R’den R ye

Binom açılımı nedir ve nasıl ifade edilir, kullanılan denklemler, formüller nelerdir? Binom açılımı formülleri, hesaplanması, terim katsayıları. Binom açılımı, aslında bir çarpma işlemini düzenli şekilde yazmanın yoludur. İki terimli bir ifadeyi (mesela (a + b) gibi) birkaç kez kendisiyle çarptığımızda, ortaya birçok terim çıkar. İşte bu terimlerin sistemli ve düzenli bir şekilde sıralanmasına binom açılımı

Bir Küre İle Bir Düzlemin Kesişimi, arakesiti ile ilgili özellikleri, örnek soru ve çözümleri hakkında bilgi. Bir Küre ile Bir Düzlemin Arakesiti Bir küre yüzeyinin bir düzlem ile ara kesiti bir çember, kürenin bir düzlem ile ara kesiti ise bir dairedir. Şekildeki O merkezli küre ile P düzleminin ara kesiti A merkezli dairedir. Küre merkezinin

Bir sayının sıfır ile çarpımı kaç sonucunu verir? Sayıların sıfır ile çarpılması, bölünmesi, sayıların sıfıra bölünmesinin hesaplanması Bir Sayının Sıfır İle Çarpımı Kaçtır? Matematikte çarpmada sıfır yutan elemandır. Yutan eleman kendine çeviren, yiyen eleman anlamındadır. Sıfır da çarpma işleminin sonucunu kendine çevirir. O halde bir sayının sıfır ile çarpımı sıfır sonucunu verir. Buradaki sayının, negatif,

Geometrik ortalama nedir ve hangi durumlarda, nasıl hesaplanır? Geometrik ortalamanın formülü nasıldır? Geometrik ortalama örneklerle hesaplaması Geometrik Ortalama Geometrik ortalama, genellikle nüfus artışı veya faiz oranları gibi büyüme oranları için kullanılan bir ortalama türüdür. Aritmetik ortalama öğeleri eklerken, geometrik ortalama öğeleri çarpar. Ayrıca, sadece pozitif sayılar için geometrik ortalama elde edebilirsiniz. Teknik olarak “n sayısının

Harmonik ortalama nedir, ne amaçla ve nasıl hesaplanır? Harmonik ortalamanın formülü nasıldır? Harmonik ortalama örnekleri hesaplaması. Harmonik Ortalama Nedir? Harmonik ortalama bir nümerik ortalama türüdür. Harmonik ortalama, bir sayı kümesinin ortalamasını hesaplamak için kullanılır. Eleman sayısının ortalaması alınır ve elemanların karşılıklarının toplamına bölünür. Gözlem sayısının, gözlemin karşılıklı toplamına bölünmesiyle hesaplanır. 1,4 ve 4’ün harmonik ortalaması:

Aritmetik ortalama nedir, neyi ifade eder ve nasıl hesaplanır? Aritmetik ortalamanın formülü, kullanım alanları ve örnek hesaplaması. Aritmetik Ortalama Aritmetik ortalama, ortalamanın en basit ve en yaygın kullanılan ölçüsüdür. Sadece bir grup sayının toplamını almayı, ardından bu toplamı seride kullanılan sayıların sayısına böler. Örneğin, 34, 44, 56 ve 78’i alın. Toplam 212’dir. Aritmetik ortalama 212

2. Dereceden Denklemin Köklerinin Karmaşık Sayı İle İlişkisi nedir, örneklerle konu anlatımı, hakkında bilgi, örnek sorular ve çözümler. II. DERECE DENKLEMİN KÖKLERİNİN KARMAŞIK SAYI İLE İLİŞKİSİ a, b, c ∈ ve a ≠ O olmak üzere, ax +bx+c = 0 denkleminde  ise II. derece denklemin kökleri birbirinin eşleniğidir. x1 = x + iy ve x2 =