Logaritmada kuvvet kuralı, logaritma fonksiyonunu daha anlaşılır hale getiren bir stratejidir. Bu makalede logaritmada kuvvet kuralını açıklıyor ve örneklerle nasıl kullanılacağını gösteriyoruz.
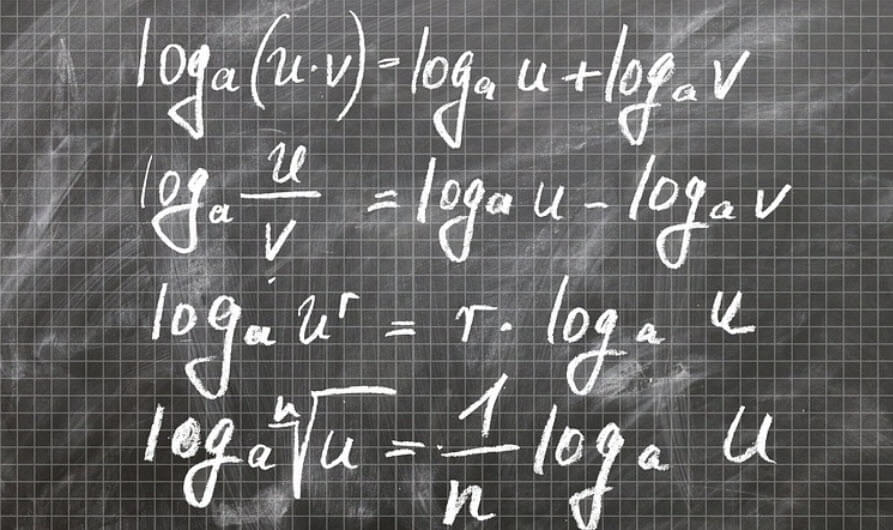
Kaynak: pixabay.com
Logaritma kuvvet kuralı, logaritmanın kuvvetini başka bir sayının logaritmasına dönüştüren bir kuraldır. Bu kural, logaritmanın çarpma ve bölme işlemlerinde nasıl davrandığını ifade eder. Logaritmanın kuvvet kuralı şu şekildedir:
- Kural: logₐ (x^m) = m * logₐ (x)
Bu kurala göre, bir sayının üssü alındıktan sonra logaritması alınıyorsa, sonuç olarak bu sayının logaritması ile üssünün çarpımı elde edilir. Örneklerle açıklayalım:
Örnek 1: log₂ (8³) hesaplayalım. Burada 8’in üssü 3 olduğu için, 8³ = 8 * 8 * 8 = 512 olur. Kurala göre, log₂ (8³) = 3 * log₂ (8) şeklinde yazabiliriz. log₂ (8) = log₂ (2³) olduğu düşünülerek, 3 * log₂ (2³) = 3 * 3 = 9 elde ederiz.
Örnek 2: log₅ (125⁴) hesaplayalım. Burada 125’in üssü 4 olduğu için, 125⁴ = 125 * 125 * 125 * 125 = 1,953,125 olur. Kurala göre, log₅ (125⁴) = 4 * log₅ (125) şeklinde yazabiliriz. 5³ = 125 olduğu için, 4 * log₅ (5³) = 4 * 3 = 12 elde ederiz.
Bu şekilde logaritmada kuvvet kuralını kullanarak verilen ifadeleri daha basit bir şekle dönüştürebilir ve işlemleri daha kolay hale getirebiliriz. Kuralı doğru bir şekilde uygulayarak örnekler üzerinde pratik yaparak konuyu daha iyi anlayabilirsiniz.
Logaritmanın Özellikleri: Çoklu Adımlar
Logaritmanın birçok özelliği bulunmaktadır. İşte logaritmanın bazı önemli özellikleri:
- logₐ (1) = 0: Herhangi bir sayının 1’e göre logaritması her zaman 0’dır. Yani logₐ (1) = 0.
- logₐ (a) = 1: Herhangi bir sayının kendi tabanına göre logaritması her zaman 1’dir. Yani logₐ (a) = 1.
- logₐ (x * y) = logₐ (x) + logₐ (y): İki sayının çarpımının logaritması, bu sayıların a tabanına göre logaritmalarının toplamına eşittir. Yani logₐ (x * y) = logₐ (x) + logₐ (y).
- logₐ (x / y) = logₐ (x) – logₐ (y): İki sayının bölümünün logaritması, bu sayıların a tabanına göre logaritmalarının farkına eşittir. Yani logₐ (x / y) = logₐ (x) – logₐ (y).
- logₐ (x^m) = m * logₐ (x): Bir sayının üssünün logaritması, bu sayının a tabanına göre logaritmasının üssine eşittir. Yani logₐ (x^m) = m * logₐ (x).
- logₐ (b) = logₓ (b) / logₓ (a): Bir sayının a tabanına göre logaritması, aynı sayının başka bir tabana göre logaritmasıyla tabanların logaritmalarının oranına eşittir. Yani logₐ (b) = logₓ (b) / logₓ (a).
Bu özellikler, logaritmalarla ilgili işlemleri daha kolay hale getirir ve logaritma denklemlerini çözmede yardımcı olur. Logaritmanın diğer özellikleri de bulunmakla birlikte, bu özellikler genellikle en sık kullanılan ve temel olarak kabul edilenleridir.
Logaritma Çarpım Kuralının İspatı
Logaritma çarpım kuralını ispatlamak için aşağıdaki adımları takip edebiliriz:
Verilen ifade: logₐ (x * y) = logₐ (x) + logₐ (y)
Adım 1: logₐ (x * y) = n olarak kabul edelim.
Adım 2: Bu durumda, aᵏ = x * y şeklinde ifade edebiliriz, burada k logaritmanın tabanı olan a’ya karşılık gelir.
Adım 3: x * y = aⁿ olduğunu göz önünde bulundurarak, x ve y’yi a’ya dönüştürebiliriz: x = aᵖ ve y = aᑕ şeklinde yazabiliriz.
Adım 4: Bu durumda, aⁿ = aᵖ * aᑕ olacaktır.
Adım 5: logₐ (aⁿ) = logₐ (aᵖ * aᑕ) şeklinde yazarak, logaritma çarpım kuralını kullanarak ifadeyi yeniden düzenleyebiliriz.
Adım 6: n = p + ᑕ olarak ifade edebiliriz.
Adım 7: Bu durumda, logₐ (x * y) = logₐ (x) + logₐ (y) eşitliği geçerli olur.
Bu şekilde logaritma çarpım kuralını ispatlamış oluruz. Adımları takip ederek, logaritma çarpım kuralının nasıl elde edildiğini göstermiş olduk. Bu kural, logaritma işlemlerinde çarpma işlemi yaparken, logaritmanın toplamına dönüştüğünü gösterir.
Logaritmada Bölüm ve Kuvvet Kurallarının İspatı
Logaritma bölüm ve kuvvet kurallarını ispatlamak için aşağıdaki adımları takip edebiliriz:
Logaritma Bölüm Kuralı: Verilen ifade: logₐ (x / y) = logₐ (x) – logₐ (y)
Adım 1: logₐ (x / y) = n olarak kabul edelim.
Adım 2: Bu durumda, aⁿ = x / y olduğunu göz önünde bulunduralım.
Adım 3: x / y = aⁿ olarak ifade edebiliriz.
Adım 4: x = aⁿ * y olarak yazabiliriz.
Adım 5: logₐ (x) = logₐ (aⁿ * y) şeklinde yazarak, logaritma çarpım kuralını kullanarak ifadeyi yeniden düzenleyebiliriz.
Adım 6: logₐ (x) = logₐ (aⁿ) + logₐ (y) şeklinde yazabiliriz.
Adım 7: n = logₐ (aⁿ) olarak ifade edebiliriz.
Adım 8: Bu durumda, logₐ (x) = n + logₐ (y) eşitliği geçerli olur.
Adım 9: logₐ (x / y) = n = logₐ (x) – logₐ (y) şeklinde yazabiliriz.
Bu şekilde logaritma bölüm kuralını ispatlamış olduk. Adımları takip ederek, logaritma bölüm kuralının nasıl elde edildiğini gösterdik.
Logaritma Kuvvet Kuralı: Verilen ifade: logₐ (x^m) = m * logₐ (x)
Adım 1: logₐ (x^m) = n olarak kabul edelim.
Adım 2: Bu durumda, aⁿ = x^m olduğunu göz önünde bulunduralım.
Adım 3: x^m = aⁿ olarak ifade edebiliriz.
Adım 4: x = (aⁿ)^(1/m) olarak yazabiliriz.
Adım 5: logₐ (x) = logₐ ((aⁿ)^(1/m)) şeklinde yazarak, logaritma kuvvet kuralını kullanarak ifadeyi yeniden düzenleyebiliriz.
Adım 6: logₐ (x) = (1/m) * logₐ (aⁿ) şeklinde yazabiliriz.
Adım 7: n = logₐ (aⁿ) olarak ifade edebiliriz.
Adım 8: Bu durumda, logₐ (x) = (1/m) * n eşitliği geçerli olur.
Adım 9: logₐ (x^m) = n = m * logₐ (x) şeklinde yazabiliriz.
Bu şekilde logaritma kuvvet kuralını ispatlamış olduk. Adımları takip ederek, logaritma kuvvet kuralının nasıl elde edildiğini gösterdik.
Logaritmaların Değerini Bulalım: Taban Değiştirme Kuralı
Taban değiştirme kuralı, bir logaritma ifadesinin tabanını değiştirmek için kullanılan bir kuraldır. Taban değiştirme kuralı şu şekildedir:
logₐ (x) = logᵦ (x) / logᵦ (a)
Bu kurala göre, bir logaritmanın tabanını değiştirmek için, logaritmanın değerini yeni tabana göre logaritma yapılıp, bu değer yeni tabanın logaritması ile eski tabanın logaritmasının oranı alınır.
Örnek olarak, log₂ (8) değerini log₅ tabanına değiştirelim.
Adım 1: Taban değiştirme kuralını kullanarak yeni tabanın logaritmasını ve eski tabanın logaritmasını bulalım: log₂ (8) = log₅ (8) / log₅ (2)
Adım 2: log₅ (8) değerini bulalım. 5 üzerinden hangi üssün 8’e eşit olduğunu bulmamız gerekiyor: 5³ = 125, 5⁴ = 625 Bu durumda, 5³ < 8 < 5⁴ olduğu için, log₅ (8) ≈ 3.292
Adım 3: log₅ (2) değerini bulalım: 2 = 5^(log₅ (2)) Bu durumda, log₅ (2) ≈ 0.431
Adım 4: Elde ettiğimiz değerleri kullanarak taban değiştirme kuralını uygulayalım: log₂ (8) ≈ log₅ (8) / log₅ (2) ≈ 3.292 / 0.431 ≈ 7.625
Sonuç olarak, log₂ (8) ≈ 7.625 olduğunu bulduk. Taban değiştirme kuralını kullanarak, logaritmanın değerini farklı bir tabana dönüştürebiliriz.
Logaritmada Taban Değiştirme Formülünü Kullanalım
Logaritmada taban değiştirme formülünü kullanarak bir örnek yapalım:
Örnek olarak, log₂ (64) değerini log₅ tabanına değiştirelim.
Taban değiştirme formülü şu şekildedir:
logₐ (x) = logᵦ (x) / logᵦ (a)
Bu formülü kullanarak adımları takip edelim:
Adım 1: log₂ (64) değerini log₅ tabanına değiştirmek istiyoruz.
Adım 2: Taban değiştirme formülünü uygulayalım: log₂ (64) = log₅ (64) / log₅ (2)
Adım 3: log₅ (64) değerini bulalım: 64 = 5^x x = log₅ (64)
64, 5’in 2. kuvvetine eşit olduğu için x = 2 olur.
Adım 4: log₅ (2) değerini bulalım: 2 = 5^y y = log₅ (2)
Bu durumda, log₅ (2) ≈ 0.4307
Adım 5: Elde ettiğimiz değerleri kullanarak taban değiştirme formülünü uygulayalım: log₂ (64) ≈ log₅ (64) / log₅ (2) ≈ 2 / 0.4307 ≈ 4.625
Sonuç olarak, log₂ (64) ≈ 4.625 olduğunu bulduk. Taban değiştirme formülünü kullanarak, logaritmayı farklı bir tabana dönüştürebiliriz.
Logaritmada Taban Değiştirme Formülünün İspatı
Logaritmada taban değiştirme formülünün ispatını yapmak için aşağıdaki adımları takip edebiliriz:
Verilen ifade: logₐ (x) = logᵦ (x) / logᵦ (a)
Adım 1: logₐ (x) = n olarak kabul edelim.
Adım 2: Bu durumda, aⁿ = x olduğunu göz önünde bulunduralım.
Adım 3: x = ᵦᵐ şeklinde ifade edebiliriz, burada m logaritmanın tabanı olan ᵦ’ye karşılık gelir.
Adım 4: aⁿ = ᵦᵐ olarak ifade edebiliriz.
Adım 5: n * logᵦ (a) = m olarak yazarak, x’in tabanını değiştirebiliriz.
Adım 6: n = logᵦ (x) ve m = logᵦ (a) olarak ifade edebiliriz.
Adım 7: Bu durumda, logₐ (x) = n = logᵦ (x) / logᵦ (a) eşitliği geçerli olur.
Bu şekilde logaritmada taban değiştirme formülünü ispatlamış olduk. Adımları takip ederek, logaritmaların tabanını değiştirme işleminin nasıl yapıldığını gösterdik.
Taban Değiştirme Kuralını Kullanarak Logaritmaların Değerini Bulalım
Taban değiştirme kuralını kullanarak logaritmaların değerini bulmak için aşağıdaki adımları takip edebiliriz:
Örnek olarak, log₃ (9) değerini log₂ tabanına değiştirelim.
Adım 1: Taban değiştirme kuralını kullanarak yeni tabanın logaritmasını ve eski tabanın logaritmasını bulalım: log₃ (9) = log₂ (9) / log₂ (3)
Adım 2: log₂ (9) değerini bulalım: 9 = 2^x şeklinde ifade edebiliriz. Buradan x = log₂ (9) olduğunu görüyoruz.
Adım 3: x’in değerini bulalım: 2^3 = 8 ve 2^4 = 16 olduğunu göz önünde bulundurursak, 9 8 ile 16 arasında yer alır. Bu durumda x ≈ 3.1699 olarak bulunur.
Adım 4: log₂ (3) değerini bulalım: 3 = 2^y şeklinde ifade edebiliriz. Buradan y = log₂ (3) olduğunu görüyoruz.
Adım 5: y’in değerini bulalım: 2^1 = 2 ve 2^2 = 4 olduğunu göz önünde bulundurursak, 3 2 ile 4 arasında yer alır. Bu durumda y ≈ 1.5849 olarak bulunur.
Adım 6: Elde ettiğimiz değerleri kullanarak taban değiştirme kuralını uygulayalım: log₃ (9) ≈ log₂ (9) / log₂ (3) ≈ 3.1699 / 1.5849 ≈ 2
Sonuç olarak, log₃ (9) ≈ 2 olduğunu bulduk. Taban değiştirme kuralını kullanarak, logaritmanın değerini farklı bir tabana dönüştürebiliriz.
Değişkenli Logaritmik Denklemler
Değişkenli logaritmik denklemler, logaritma fonksiyonunun içinde değişkenlerin yer aldığı denklemlerdir. Bu tür denklemleri çözmek için farklı yöntemler kullanılabilir. İşte bazı yaygın kullanılan yöntemler:
- Denklemi İfadeyi Sadeleştirme: Değişkenli logaritmik denklemi daha basit bir hale getirmek için denklemi ifadeyi sadeleştirebilirsiniz. İfadeyi sadeleştirmek için logaritma kurallarını kullanarak logaritma ifadesini daha basit bir hale getirmeye çalışın.
- Denklemin Tabanını Değiştirme: Eğer denklemdeki taban belirli bir değilse, denklemi daha kolay hale getirmek için taban değiştirme kuralını kullanabilirsiniz. Denklemin tabanını değiştirerek, logaritmayı farklı bir tabana dönüştürebilirsiniz ve denklemin çözümünü bulabilirsiniz.
- Eşitlik Kurma: Denklemdeki logaritma ifadesini bir değişken olarak kabul ederek, denklemi çözebilirsiniz. Eşitlik kurarak, logaritma ifadesini diğer taraf ile eşitleyebilir ve denklemi daha basit bir forma getirebilirsiniz. Bu şekilde denklemin çözümünü bulabilirsiniz.
- Grafik Yöntemi: Denklemi çözmek için logaritma fonksiyonunu grafiğini çizebilirsiniz. Grafik üzerinde denklemin çözümünü bulmak için, denklem ile logaritma fonksiyonunun grafiği kesim noktalarını bulabilirsiniz.
- Sayısal Yöntemler: Kimi durumlarda, değişkenli logaritmik denklemler analitik olarak çözülemez. Bu durumlarda, sayısal yöntemler kullanılabilir. Sayısal yöntemler, denklemin çözümünü yaklaşık olarak bulmak için iterasyon ve yaklaşım yöntemlerini kullanır.
Değişkenli logaritmik denklemler genellikle matematiksel problem çözümü ve bilimsel araştırmalarda karşımıza çıkar. Denklemleri çözmek için kullanılan yöntem, denklemin karmaşıklığına ve özel gerekliliklere bağlı olarak değişebilir.
Tabanında Değişken Olan Logaritmik Denklemler
Tabanında değişken olan logaritmik denklemler, logaritma fonksiyonunun tabanının da bir değişkene bağlı olduğu denklemlerdir. Bu tür denklemleri çözmek için aşağıda verilen yöntemleri kullanabilirsiniz:
- Eşitlik Kurma: Denklemin tabanındaki değişkeni bir değişken olarak kabul ederek, denklemi çözebilirsiniz. Eşitlik kurarak, logaritma ifadesini diğer taraf ile eşitleyebilir ve denklemi daha basit bir forma getirebilirsiniz. Bu şekilde denklemin çözümünü bulabilirsiniz.
- Taban Değiştirme: Eğer denklemin tabanı belirli bir değilse, taban değiştirme kuralını kullanabilirsiniz. Denklemin tabanını değiştirerek, logaritmayı farklı bir tabana dönüştürebilirsiniz ve denklemin çözümünü bulabilirsiniz. Ancak, bu yöntem bazı durumlarda karmaşık sonuçlara yol açabilir.
- Grafik Yöntemi: Denklemi çözmek için logaritma fonksiyonunun ve tabanındaki değişkenin grafiğini çizebilirsiniz. Grafik üzerinde denklemin çözümünü bulmak için, denklem ile logaritma fonksiyonunun grafiği kesim noktalarını bulabilirsiniz. Bu yöntem grafiksel çözüm sağlar, ancak kesirli, karmaşık veya negatif değerlerle ilgili bazı sınırlamaları vardır.
- Sayısal Yöntemler: Tabanında değişken olan logaritmik denklemleri çözmek için sayısal yöntemler kullanılabilir. Bu yöntemler, denklemin çözümünü yaklaşık olarak bulmak için iterasyon ve yaklaşım yöntemlerini kullanır. Bu tür denklemler genellikle analitik olarak çözülemez ve sayısal yöntemler daha uygun olabilir.
Tabanında değişken olan logaritmik denklemler genellikle matematiksel modellemelerde, mühendislik problemlerinde veya bilimsel araştırmalarda ortaya çıkabilir. Denklemi çözmek için en uygun yöntemi seçmek, denklemin karmaşıklığına, tabandaki değişkenin özelliklerine ve çözümün gerekliliklerine bağlı olacaktır.