12. sınıf geometri konusu, iki noktadan geçen bir doğrunun denklemi nedir, nasıl hesaplanır, iki noktadan geçen doğru denklemi örnek sorular ve çözümleri.

Uzayda İki Noktadan Geçen Doğru
Uzayda iki noktadan geçen doğru, matematik ve geometri alanında önemli bir konudur. Bu doğru, iki farklı noktadan geçerek uzayı kesen bir doğrudur.
Uzayda iki noktadan geçen doğru, iki noktanın koordinatlarının kullanıldığı bir yöntemle hesaplanabilir. İki noktanın koordinatları kullanılarak doğrunun denklemi türetilebilir. Bu doğru denklemi, yön vektörü ve bir noktanın koordinatlarından oluşur.
Bir yön vektörü, doğrunun yönünü ve eğimini belirler. Bu vektör, iki noktanın koordinatları arasındaki fark vektörüdür. Bu fark vektörü, doğrunun yönünü ve eğimini belirler.
Uzayda iki noktadan geçen doğru, uzayda hareket eden cisimlerin konumunu belirlemek ve yönünü belirlemek için kullanılabilir. Özellikle uzayda seyahat eden araçların konumlarının tespiti için bu doğru kullanılır.
Uzayda iki noktadan geçen doğru, matematiksel modellerin yanı sıra, uzay teknolojisi ve navigasyon sistemleri gibi birçok alanda da kullanılır.
Örnek:
Taban düzlemi, xOy düzlemi olan koordinat sisteminde (1,2,3) noktası ile (-1,3,0) noktasından geçen doğrunun denklemi istenildiğinde, şu adımlar takip edilebilir:
- İki nokta arasındaki fark vektörü bulunur: (1-(-1), 2-3, 3-0) = (2, -1, 3)
- Bu fark vektörü doğru üzerinde bir noktayı belirlemek için kullanılır. Örneğin, (1,2,3) noktasını kullanalım.
- Doğru denklemi yön vektörü ve bir noktanın koordinatları kullanılarak yazılır:
x – 1 y – 2 z – 3 —— = —— = —— 2 -1 3
Bu doğru denklemi, uzayda bu iki noktadan geçen doğruyu ifade eder.
Ayrıca, bu doğru denklemi parametrik formda da yazılabilir. Bu durumda, doğru x = 1 + 2t, y = 2 – t ve z = 3 + 3t şeklinde ifade edilebilir. Burada, t parametresi doğrunun herhangi bir noktasının koordinatları için seçilebilir. Örneğin, t = 0 için doğrunun (1,2,3) noktasına karşılık gelir, t = 1 için doğrunun (3,1,6) noktasına karşılık gelir.
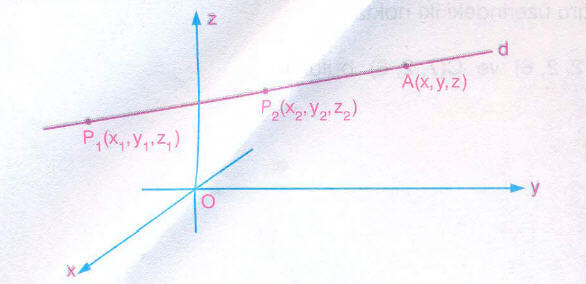
Denklemi
Uzayda, ve
noktalarından geçen doğrunun denklemi,
Örnek:
Analitik uzayda, K(2, -3,1) ve L(3, 5, 4) noktalarından geçen doğrunun denklemini bulalım.
Çözüm:
- K(2, -3,1), L(3, 5, 4) noktalarından geçen doğrunun denklemi
k ∈ R bulunur.
Not
Uzayda, noktasından geçen ve doğrultmanı v = (a, b, c) olan doğrunun standart denklemi,
Bu denklemden, doğrunun parametrik denklemi,
- x = x1 + ak
- y = y1 + bk
- z = z1 + ck
doğrunun vektörel denklemi, bulunur.
Örnek:
Analitik uzayda, A(-3,2, 7) ve B(2, -4,5) noktalarından geçen doğrunun doğrultman vektörünü bulalım.
Çözüm:
A ve B noktalarından geçen doğrunun doğrultman vektörü
bulunur.