Çemberde Benzerlik Formülleri, Özellikleri, Çözümlü Örnek Sorular
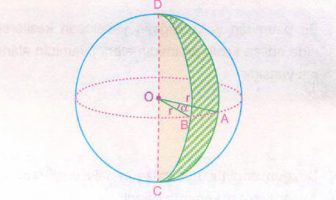
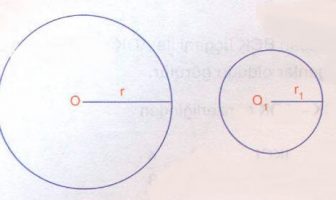
Çemberde Benzerlik nedir? Çemberde benzerlik özellikleri ve formülleri nelerdir? Çemberde benzerlik konu anlatımı, örnek soru çözümleri. Çemberde Benzerlik Bütün çemberler benzerdir. Merkez açıları eşit olan bütün çember yaylarıda benzerdir. Çevreleri oranı benzerlik oranına eşittir. Benzerlik oranı dir. Örnek |OD| = 2.|BD| |DC| = 12 cm O noktası her iki çemberin merkezidir. Buna göre, |AB| kaç