Dikey Asimptot Nasıl Bulunur? Hesaplanması Örnek Soru Çözümleri

Dikey Asimptot nedir, nasıl bulunur? Dikey Asimptot hesaplanması, çözümleriyle soru örnekleri, çözümler, grafikleri, ve örnekler..

Dikey Asimptot Nedir?

Bir asimptot, belirli bir eğriye keyfi olarak yaklaşan bir çizgi veya eğridir. Başka bir deyişle, belirli bir eğriye yakın bir çizgidir, öyle ki eğri ile çizgi arasındaki mesafe, eğri daha yüksek / düşük değerlere ulaştığında sıfıra yaklaşır. Asimptotlu eğrinin bölgesi asimptotiktir. Asimptotlar genellikle rotasyonel fonksiyonlarda, üstel fonksiyonda ve logaritmik fonksiyonlarda bulunur. Y eksenine paralel asimptot, dikey asimptot olarak bilinir.

Dikey Asimptotun Belirlenmesi

Bir f (x) fonksiyonu asimptotlara sahipse, fonksiyon bazı sonlu C değerlerinde aşağıdaki koşulu karşılar.

i. f(C) = Tanımsız ⇒
fonksiyon C’de tanımlanmamıştır, bu nedenle C, f’nin etki alanında değildir
ii. $\displaystyle \underset{{x\to {{c}^{+}}}}{\mathop{{\lim }}}\,f\left( x \right)=\pm \infty$ ve $\displaystyle \underset{{x\to {{c}^{-}}}}{\mathop{{\lim }}}\,f\left( x \right)=\pm \infty$
C’ye yaklaşan fonksiyon, negatif ve pozitif sonsuzluğa meyillidir.

Genel olarak, bir fonksiyon sonlu bir değerde tanımlanmamışsa, bir asimptota sahiptir. Bununla birlikte, bir noktada tanımlanmamış bir fonksiyon, fonksiyon özel bir şekilde tanımlanmışsa, bu değerde bir asimptota sahip olmayabilir. Bu nedenle sonlu değerlerde limitler alınarak teyit edilir. Sonlu değerlerdeki (C) sınırlar sonsuza eğilimliyse, fonksiyonun C de x = C denklemi ile bir asimptoti vardır.

Dikey asimptotlar nasıl bulunur – Örnekler

1. F (x) = 1 / x olarak düşünün

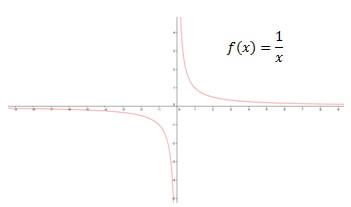
Dikey asimptot

F (x) = 1 / x fonksiyonunun hem dikey hem de yatay asimptotları vardır. f (x) 0’da tanımlanmamıştır. Bu nedenle, limitlerin 0’da alınması onaylanacaktır.

$\displaystyle \underset{{x\to {{0}^{+}}}}{\mathop{{\lim }}}\,\frac{1}{x}=+\infty$ ve
$\displaystyle \underset{{x\to {{0}^{-}}}}{\mathop{{\lim }}}\,\frac{1}{x}=-\infty$

Farklı yönlerden yaklaşan işlevin farklı sonsuzluklara yöneldiğine dikkat edin. Negatif yönden yaklaşırken, fonksiyon negatif sonsuzluğa eğilim gösterir ve pozitif yönden yaklaşırken fonksiyon pozitif sonsuzluğa eğilim gösterir. Bu nedenle, asimptotun denklemi x = 0’dır.

2. F (x) = 1 / (x-1) (x + 2) fonksiyonunu düşünün

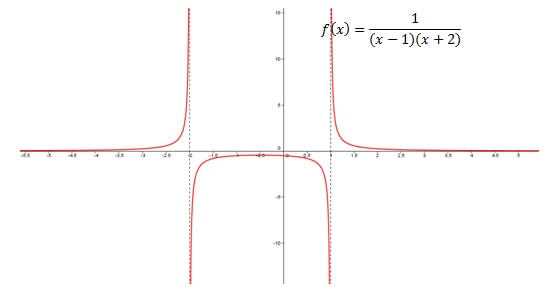
Dikey asimptot

Fonksiyon, x = 1 ve x = -2’de mevcut değildir. Bu nedenle, x = 1 ve x = -2’de limit alırsak,
$\displaystyle \underset{{x\to {{1}^{+}}}}{\mathop{{\lim }}}\,\frac{1}{{\left( {x-1} \right)\left( {x+2} \right)}}=+\infty$ ve
$\displaystyle \underset{{x\to {{1}^{-}}}}{\mathop{{\lim }}}\,\frac{1}{{\left( {x-1} \right)\left( {x+2} \right)}}=-\infty$
Bu nedenle, fonksiyonun x = 1 ve x = -2’de dikey asimptotlara sahip olduğu sonucuna varabiliriz.

3. $\displaystyle f\left( x \right)=3{{x}^{2}}+\frac{{{{e}^{x}}}}{{\left( {x+1} \right)}}$ fonksiyonunu düşünün.

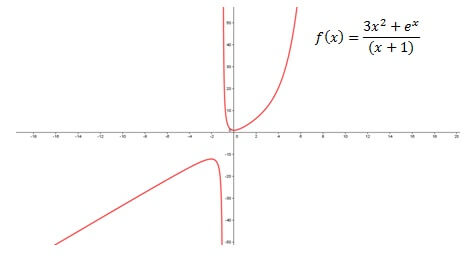
Dikey asimptot

Bu fonksiyon hem dikey hem de eğik asimptotlara sahiptir, ancak fonksiyon x = -1’de yoktur. Bu nedenle, asimptot varlığını doğrulamak için sınırlar x = -1 olarak alınır.

$\displaystyle \underset{{x\to -{{1}^{+}}}}{\mathop{{\lim }}}\,\frac{{3{{x}^{2}}+{{e}^{x}}}}{{\left( {x+1} \right)}}=+\infty$ ve
$\displaystyle \underset{{x\to -{{1}^{-}}}}{\mathop{{\lim }}}\,\frac{{3{{x}^{2}}+{{e}^{x}}}}{{\left( {x+1} \right)}}=-\infty$
Bu nedenle, asimptot denklemi x = -1’dir.
Eğik asimptoti bulmak için farklı bir yöntem uygulanmalıdır.