Thales teoremi nedir? Thales teoremi nasıl hesaplanır, açıklanması, formülleri ve ispatlaması, kesişim teoremi, örnekler.
Thales Teoremi
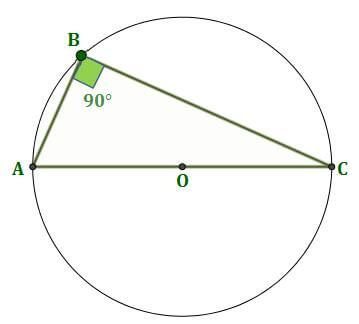
Thales Teoremi, yazılı açı teoreminin özel bir halidir, bir çevreye yazılan dik üçgenlerle ilgilidir. Thales teoremi, eğer A, B ve C, AC çizgisinin bir çap olduğu O merkezli (çevre merkezi) bir daire üzerinde farklı noktalarsa, Δ ABC üçgeninin B noktasında bir dik açıya (90 ) sahip olduğunu belirtir. Böylece, Δ ABC bir dik üçgendir.
Başka bir deyişle, bir dairenin çapı her zaman daire üzerindeki herhangi bir noktaya dik açı yapar.
 Thales Teoreminin Kanıtı
Thales Teoreminin Kanıtı
O çevre merkezini B noktasına bağlarsak, her ikisi de ikizkenar üçgen olan iki üçgen Δ ABO ve Δ OBC oluştururuz çünkü tüm yarıçaplar eşittir (OA, OB ve OC eşittir). Ve taban açısı teoremine göre taban açıları eşittir. Δ ABO ‘α’ ve Δ ABO ‘β’ taban açılarını etiketleyelim.
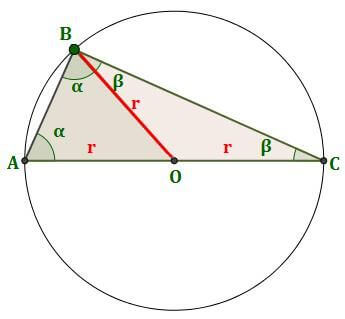
İkizkenar üçgen olduklarından, her birinin iki eşit açısı vardır: α ve β.
Herhangi bir üçgende olduğu gibi, Δ ABC üçgeninin iç açılarının toplamı 180°’dir:
Eşitliği 2’ye bölmek:
α + β, Δ ABC’nin B noktasındaki açısı olduğundan, Thales teoremi ispatlanmıştır.
Kesişim Teoremi
Bir takım paralel doğrular herhangi iki kesen üzerinde karşılıklı orantılı parçalar ayırır.
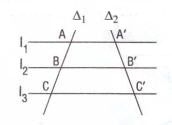
paralelleri kesen doğrular ise;
Sonuçlar:
Sonuç 1
Bir takım paralel doğrular, bunları kesen bir doğru üzerinde eşit parçalar ayırır ise, her kesen üzerinde eşit parçalar ayırır.
orantısından
Sonuç 2
Doğru parçalarının uzunlukları arasında ,orantısı var ise;
orantısı vardır.
Bir açının kenarları arasında kalan paralel iki doğru parçasının oranı, bu paralellerin bir kenarı kestiği iki noktanın açının köşelerine kadar olan uzaklıklarının oranına eşittir.
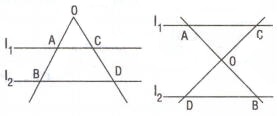
Sonuç 3:
Bir üçgenin bir kenarına çizilen paralel doğru diğer iki kenarı içten veya dıştan aynı oranda böler.
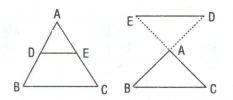
üçgenlerinde
ise;
olur.