Cebir nedir ne demektir? Cebirin esasları, denklem kurma ve denklem çözümleri ile ilgili olarak genel bilgilerin yer aldığı yazımız.
Bize sayıları, bunların özelliklerini, aralarında yapılan işlemleri aritmetik öğretir. Cisimlerin çizgileriyle, yüzeyleriyle, hacimleriyle ilgili özelliklerini inceleyip ölçen bilim dalına da geometri diyoruz. Aritmetikle geometri, ikisi bir arada matematik adını alır. Bu konularda işlemler yaparken hep sayılarla uğraştık, rakamlarla işlemler yaptık. Yalnız, matematik işlemlerinde rakam yerine harf kullanıldığı da olur. İşte matematiğin çok meraklı, ilgi çekici bir koluna geliyoruz: Cebir.
CEBİR NEDİR?
Cebir matematiğin formüllerle, denklemlerle, basitleştirilmiş şeklidir. Bundan dolayı ona, «matematiğin kısa yazılışı» denebilir. Cebirin ne olduğunu anlayabilmek için, temele inelim; işe «harfli ifadeler»le başlayalım.
Harfli İfade.
Sayılarla yaptığımız bütün işlemleri harflerle, (harfli ifadelerle) de yapabiliriz. Bir ifade içinde hem sayı, hem de harf varsa buna harfli ifade deriz. 5a , a + b + c , 2a+2b , 2r , πr² hep harfli ifadedir.
- Harfli ifadeler en çok formüllerde kullanılır.
Bir örnek: Bir çemberin uzunluğunun yarıçapı ile π (pi) sayısının çarpımının iki katına eşit olduğunu biliyoruz. Bu eşitliği böyle sözle uzun uzun anlatmak yerine, belli harflere belli anlamlar veririz; sonra da formülü yazarız. Formül bizim sözle anlattığımızı kısaca anlatıverir. Çemberin yarıçapı her zaman r ile gösterilir. Çember uzunluğuna da m dersek, yukarıdaki uzunluk ifadesi şu şekli alır:
- m = 2πr
Gene böyle, «dairenin alanı, yarıçapının karesinin n ile çarpımına eşittir» değil mi? Bunu anlatmak için şu formülü yazarız:
- S = πr²
- Aritmetikteki, geometrideki, fizik-kimyadaki bütün eşitlikler formüllerle gösterilir. Böylece işimiz kolaylaşır.
Katsayı.
Bir harfli ifade’de, harfin yanındaki çarpana katsayı denir. Örnek: 8a harfli ifadesinde 8 sayısı a harfinin katsayısıdır. Hem 8, hem de a çarpan’dır. Tek terimli harfli ifadeler olduğu gibi çok terimli harfli ifadeler de vardır.
Örnek: 8a tek terimli bir harfli ifadedir. Buna karşılık a² + 2ab + b² harfli ifadesi üç terimlidir. Birbirinden + (artı), ya da — (eksi) işaretiyle ayrılmış çarpanlardan oluşan terimler de aralarında toplanır, çıkarılır, çarpılır, bölünür. Toplama çıkarma için benzer terimler alınır, katsayıları toplanır. Böylece tek terim elde edilir.
Örnek:
- 3a+7b—4a+2a—6b + 5a + 9b = 6a+ 10b
CEBİRİN ESASLARI
Burada, dikkat edileceği gibi, harflerin katsayıları işaretleriyle birlikte düşünülmüştür.
- • Cebirde sabit sayıların da, harfli ifadelerin de işaretleri hiçbir zaman gözden uzak tutulmaz.
- • Cebirde işaretsiz terim yoktur.
- Bir sayının, ya da harfli bir ifadenin önünde hiçbir işaret yoksa + varmış gibi işlem yapılır.
- İki ifade birbirine eşitse bu iki ifade aralarına bir = işareti konularak yazılır: 2a + 5b = 8c + 10d gibi.
- Bazı durumlarda harfli bir ifade sabit bir sayıya eşittir. O zaman eşitliği sağlayan harf için belli bir değer belirlenmiş demektir. Örnek: 25a = 100 eşitliği verilmişse, bu eşitlik yalnız a = 4 için doğrudur.
Denklem.
Bu gibi eşitliklere denklem denir. Denklem cebirin temel tanımlarından biridir, aritmetikte çok güç çözebildiğimiz problemleri bile kolayca çözmemizi sağlar. Eşitliği gerçekleştiren değerine denklemin kökü denir. Bir denklemin kökünü bulmak için yaptığımız işlemlere ise denklemi çözmek deriz. Denklemlerde, denklemi sağlayan harf a, b, c… yerine genellikle x, y, z ile gösterilir. Buna karşılık a, b, c gibi harfler sabit büyüklükleri belirtir.
Şöyle bir örnek alalım: 3x — 6b = 0
DENKLEM ÇÖZÜMÜ
Bu bir denklemdir, b sabit bir sayıdır. x ise bilinmeyendir. Denklemi çözelim; yani bu eşitliği sağlayan x değerini bulalım. Burada unutamayacağımız bir kuralı kullanırız:
- • Bir eşitliğin bir yanından öteki yanına geçirilen ifadelerin işareti değişir: İşaret + ise — olur; — ise + olur.
Şimdi denklemi çözmeye başlayalım:
x’li ifadeyi eşitliğin bir yanında yalnız bırakmak için x’siz ifadeyi eşitliğin sağ yanına geçiririz. İşareti — iken + olur: 3x = 6b. Demek üç tane x, 6 tane b’ye eşitmiş. Biz tek x’in değerini aradığımıza göre eşitliğin her iki yanını da 3’e böleriz.
Burada da şu kuralı kullanmış oluruz: Bir eşitliğin iki yanındaki bütün terimleri aynı sayıyla çarparsak, ya da aynı sayıya bölersek eşitlik bozulmaz. Biz burada aynı sayıya yani 3’e bölüyoruz. Böylece x’in değerini bulmuş, yani denklemi çözmüş oluruz.
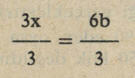
Demek ki x yerine 3 koyarsak yukarıda aldığımız denklem sağlanır, yani eşitlik olur. x yerine başka bir sayı koyarsak eşitlik bozulur. x’in bulduğumuz bu 3 değerine ilk aldığımız denklemin kökü denir. Öyleyse bizim denklemi çözmemiz, denklemin kökünü bulmak demektir.
DENKLEM KURMA
Her denklem için birçok problem söylenebilir; cebirde ise biz genellikle bunun tersiyle karşılaşırız. Bize bir problem sorarlar. Biz o problemin denklemini kurar, çözeriz. Denklemin kökü problemin çözümü olur.
Örnek olarak bir problem ele alalım: Bir koyun sürüsündeki koyunlardan 40 tanesi yavrulayınca sürünün toplamı 120 oluyor. Kuzular doğurmadan önce sürüde kaç koyun vardı?
Denklem:
Bizden sorulana x diyelim. Demek oluyor ki kuzular doğurmadan önce x koyun varmış. Bunlardan 40 tanesi kuzuladığına göre toplam x + 40 olacaktır. Bize bu toplamı da vermişler: 120 imiş. öyleyse artık denklemi kurabiliriz:
- x + 40 = 120
- Denklemin çözümü: x’i yalnız bırakmak için 40’ı eşitliğin sağ yanına geçiririz. İşareti + iken — olur:
- x = 120 — 40 = 80
Demek ki: Sürüde önce 80 koyun varmış, bunların 40 tanesi birer kuzu doğurmuş; sürü, toplam olarak 120 koyunla kuzuya çıkmış.
Sağlama: İlk denklemi alıp x yerine 40’tan başka bir sayı koyalım, örneğin 50. Bu durumda eşitliğin bozulması gerekir. Çünkü ancak denklemin kökü olan 40 eşitliği gerçekleştirir. 50 + 40 — 90 eder, oysa eşitliğin sağ yanı 80’dir. 50 kök değildir.
Kaynak – 2
Cebir, sayılardan başka simgeler de kullanılarak denklem kurma yoluyla aritmetik işlemlerini genelleştiren matematik koluna verilen genel isimdir. 9. yüzyıldan sonra özellikle Araplar ve Yunanlıların denklemle açıklamaya çalıştıkları geometriyi sayısal açıdan görmeye başladılar ve giderek denklem çözümlerinden bir hesaplama yöntemi formüle ettiler. Elementer cebir adı verilen bu yöntemi Harezmi adlı Türkistanlı bilgin bir ifadenin bir elemanından bir başka elemanına ya da bir yanından öbür yanına el cebr (zorla-zorlayışla) geçmek olarak tanımladı ve adını da buradan aldı. Bilinen en eski cebir kitabı da Harezmi’nin 830’da yazdığı Hisabül Cebr v’el Mukabe’dir (Cebir ve Karşılaştırmalı Hesabı).
Cebirin Avrupa’da tanınmasını da Türk ve Arap bilginleri sağladı. Venedikli Luca Pacolini, Avrupa’ da ilk cebir kitabını 1494’te yayımladı. Fransız Viete ise işlemlerde bilinmeyen yerine harflerin konulması kuralını getirdi. Cebirde ilk üs imlerini kullanan ve buna ilişkin ilkeleri geliştiren Descartes oldu.
Cebir, aritmetiği tersine sayıları sıfıra göre gösterir. Aritmetikte sayılar bir şeyin niceliğini, büyüklüğünü uzaklığını bildirirken cebirsel sayılarda bununla birlikte değerlendirmeyi genelleştirip kolaylaştıran iki sayı vardır; (+) pozitif, (-) negatif sayılar. Bir cebirsel işlemde sayıların önündeki (+) ve (-) işaretleri dikkate alınmadan taşıdığı değere sayının mutlak değeri adı verilir. Herhangi bir problemin genelleştirilmiş biçimine formül denilir ve aritmetikte 4 işlemle oran, orantı, çarpanlara ayırma vb gibi işlemler yardımıyla çözümlenen denklemleştirme ise formüldeki bilinmeyenin bulunması için tutulan yoldur. 16. yüzyıldan sonra günümüzdeki imlerin kullanılmaya başlandığı cebir, 3 ve 4 dereceli bilinmeyenli denklemlerin çözümlenmeye başladığı 17. yüzyılda klasik yüksek cebir ve 19. yüzyıl başlarında da modern cebir halini aldı.