Batlamyus (Ptolemy) Teoremi nedir, nasıl ortaya çıkmıştır? Teoremi kullanarak Pisagor ve altın oranın ispatı ve kullanım alanları.
Batlamyus teoremi, ‘Herhangi bir çemberdeki dörtgen için, köşegenlerinin çarpımı, her iki karşıt tarafın çarpımının toplamına eşittir’ şeklindedir. Teorem, bir beşgenin kenarları ile köşegen arasındaki altın oran ilişkisini ve Pisagor teoremini, kanıtlanmak için daha da genişletilebilir.
Michelangelo’nun Kutsal Ailesi ve Salvador Dali’nin Son Akşam Yemeği’nin ortak yönlerini hiç merak ettiniz mi?
Sanatsal harikalar olmalarının yanı sıra, bunların hepsi ortak bir tasarım felsefesini / öğesini takip ediyor. Her biri bir beşgen biçimini içerir ve herhangi bir düzenli beşgen tarafının köşegenine oranı ‘Altın Oran’ı (1.618033…) verir. Yapımlarında altın oranı izleyen insan yapımı yapılar ve doğal eşyalar, dünyadaki en estetik açıdan hoş olan şeylerden biri olarak kabul edilir.
Bir beşgenin köşegenleri ve kenarları arasındaki bu estetik ilişki, Plotemy’nin çemberde dörtgen Teoremini genişleterek kanıtlanabilir. Bununla birlikte, Ptolemy Teoremi Pisagor teoremini kanıtlamak için de kullanılabilir, ancak tüm bunlara ulaşmadan önce Ptolemy Teoremi nedir?
Batlamyus Teoremi
Claudius Ptolemy, birçok alanda uzmanlığa sahip bir Yunan efsanesiydi; astronomi (Ptolemaic sistem) çalışmalarında popüler olmasının yanı sıra, aynı zamanda derin bir matematik sihirbazıydı ve şimdi ‘Ptolemy’nin Teoremi (Batlamyus Teoremi)’ olarak bilinen bir teorem keşfetti.
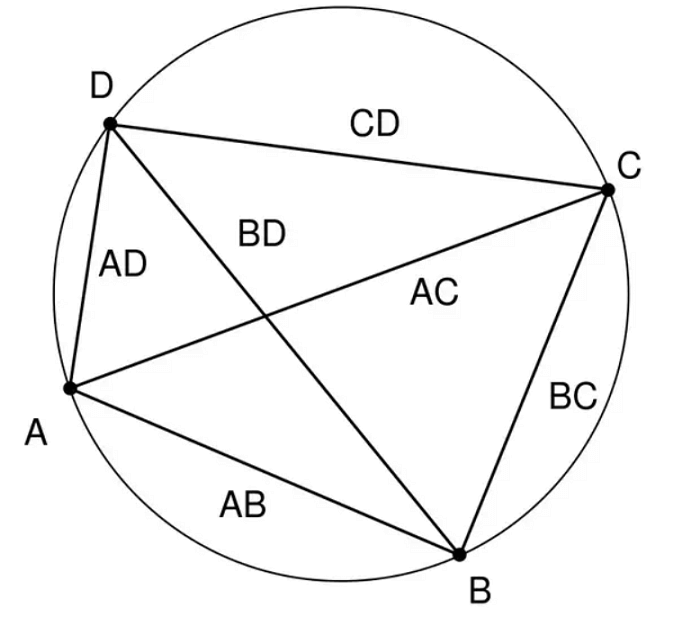
Batlamyus Teoremi şöyle der: “Bir daireye yazılan bir dörtgen için, her iki karşılıklı taraftaki ürünlerin toplamı, iki köşegeninin ürününe eşittir”.
Tüm köşeleri, yani bir daire üzerinde yatan A, B, C, D ile dörtgen bir ABCD’yi düşünün, böylece çemberde bir dörtgen oluşturun. AC ve BD, dörtgenlerin köşegenleridir, diğer tüm çizgi segmentleri (AB, BC, CD, AD) yanlarıdır. Şimdi, Ptolemy Teoremine göre, karşı tarafların ürününün (AB × CD + BC × AD) toplamı köşegenlerin ürününe (AC × BD) eşittir.
Matematiksel olarak,
- AC × BD = (AB × CD) + (BC × AD)
Yukarıdaki ilişkinin ve dolayısıyla teoremin yıllar içinde kanıtlandığı birkaç yöntem vardır. Bazı matematikçiler ilişkiyi kanıtlamak için trigonometrik kimlikler kullanırken diğerleri karmaşık sayıları veya ters geometriyi kullanır. Bununla birlikte, tüm kanıtların en basiti (bize göre) benzer üçgenlerin ve özelliklerinin kullanılmasıyla sağlanır.
Hemen hemen her matematiksel kanıtta olduğu gibi, bir şey varsayarak başlarız. Yukarıdaki çemberde dörtgen için, diyagonal AC üzerinde ∠ABK = ∠CBD olacak şekilde bir K noktası vardır.
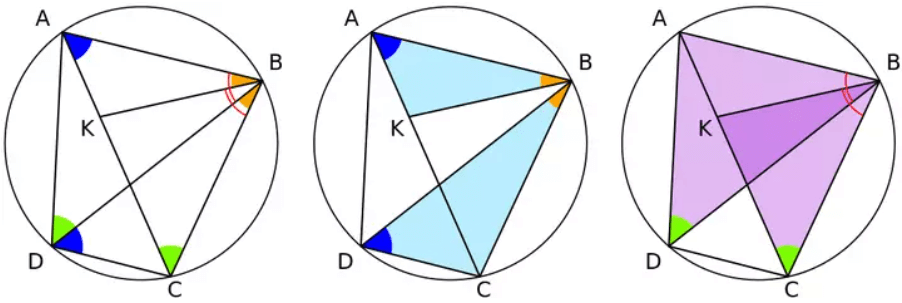
Yukarıdaki şemada görüldüğü gibi, BC yayı ∠BAC ve ∠BDC’yi ve yazılı açı teoremine göre ∠BAC = ∠BDC’yi gösterir. Benzer şekilde, AB yayı ∠ADB ve ∠ACB’yi gösterir, bu nedenle iki açı eşittir (∠ADB = ∠ACB). Benzer üçgenlerin açı-açı (AA) teoremi ile △ ABK △ DBC’ye ve △ KBC △ ABD’ye benzer.
Benzer üçgenler △ ABK ve △ DBC için:
- Buradan AKxDB = ABxDC dir.
- Benzer şekilde, benzer üçgenler △ KBC ve △ ABD için:
- Buradan KCxBD = BCxAD dir.
- Yukarıdaki denklemleri ekleyerek:
- AK.DB + KC.BD = AB.DC + BC.AD
- Burada DB ve BD aynıdır ve ortak bir kat olarak gerçekleştirilebilir,
- (AK + KC). BD = AB.DC + BC.AD
- Diyagramdan AK + KC = AC.
- Bu nedenle,
- AC.BD = AB.DC + BC.AD
İşte burada. Çemberde bir dörtgen ABCD’nin köşegenlerinin ürünü, tıpkı Ptolemy’nin Teoreminin bize söylediği gibi, karşı taraflarının ürününün toplamına eşittir!
Uygulamalar
Daha önce de belirtildiği gibi, Batlamyus Teoremi beşgenlere genişletilebilir ve yanları ve köşegenleri arasındaki altın oran ilişkisini kanıtlamak için kullanılabilir. Düzenli bir beşgen ABCDE için, kenarlar ‘a’ uzunluğunda ve köşegenler ‘d’ uzunluğundadır.
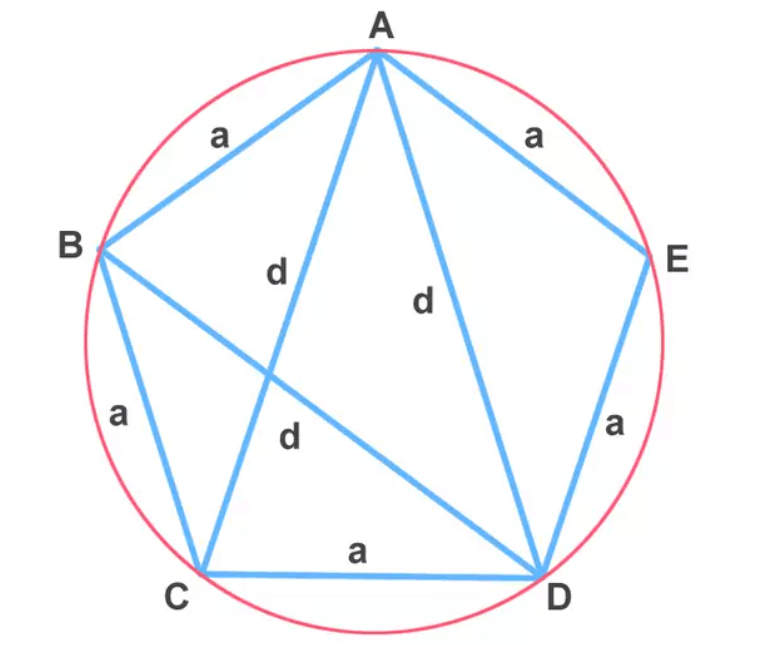
Sadece dörtgen ABCD’ye odaklanarak ve Batlamyus teoremini uygulayarak şunları elde ederiz:
- AC.BD = BC.AD + AB.DC
İlgili uzunluk değerlerini değiştirme,
- d.d = a.d + a.a
- d² = a.d + a²
Yukarıdaki denklemin a²’ye bölünmesi
- d² / a² = d / a + 1
- Şimdi, ‘d / a’ oranının ‘r’ ile temsil edilmesine izin verin
- Bu nedenle, r² = r + 1
- Yeniden düzenlenirse, r² – r – 1 = 0
- R için çözme,
- r = (1 ± √1 – 4 (1) (- 1)) / 2
- r = (1 ± √5) / 2
- r = 1.618033…
Bu nedenle, normal bir beşgenin kenarlarının köşegenlerine oranı (r = d / a = 1.618033) altın orandır. Benzer şekilde, Ptolemy Teoremini kullanarak Pisagor Teoremini kanıtlamak için, bir dairenin içine yazılmış bir ABCD dikdörtgenini hayal edin.
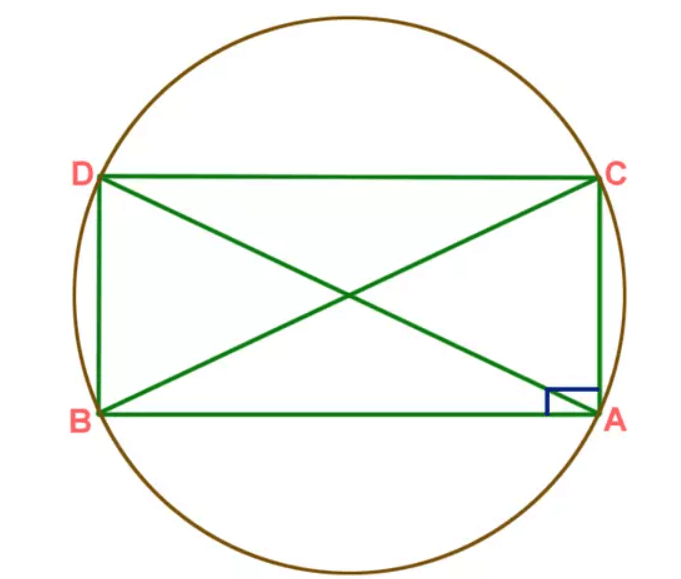
ABCD’yi dikdörtgenlemek için Ptolemy Teoremini uygulayarak,
- AD⋅BC = AB⋅DC + AC⋅DB
Herhangi bir dikdörtgen için, iki köşegen gibi karşılıklı kenarlar eşittir. Bu nedenle, AB = CD, AC = BD ve AD = BC.
- BC² = AB² + AC²
Yukarıdaki denklem, dik açılı ABC üçgenine uygulanan Pisagor Teoremi’nden başka bir şey değildir.
Son Söz
Yukarıda açıklanan iki sonuçtan başka, Ptolemy, akor tablosunu (bugün hala kullandığımız sinüs fonksiyon değerleri tablosuna benzer bir trigonometrik tablo) oluşturmak için çemberde dörtgen teoremini kullanmıştır. Türünün ilk örneği olmasa da, Ptolemy’nin akor tablosu trigonometrik fonksiyonların değerlerini 30′ artarken, Hipparchus tarafından oluşturulan ilk trigonometri tablosu 7 ° 30′ ‘lik bir artışla değerler sağladı.
Bu, çok daha doğru enterpolasyonlarla sonuçlandı ve çeşitli gezegenlerin, güneşin, ayın, yıldızların yükselişi ve yerleşiminin, ayın ve güneş tutulmalarının vs. konumlarının hesaplanmasına yardımcı oldu.
Batlamyus’un astronomik çalışmasının birleştirilmesi, toplu olarak Almagest olarak bilinen ve astronomi alanındaki en etkili çalışmalardan biri olarak kabul edilen on üç kitap şeklinde ortaya çıktı. Eserleri, önceki tüm astronomik çalışmaların yerini aldı, birkaç yıl boyunca hüküm sürdü ve bu nedenle antik çağın en büyük astronomik eseri olarak kabul edildi.