Küre yüzeyi nedir, özellikleri nelerdir? Küre yüzeyi ile ilgili doğrunun ve düzlemin konumu nasıl hesaplanır, örnekler ve formülleri hakkında bilgi.
Küre Yüzeyi
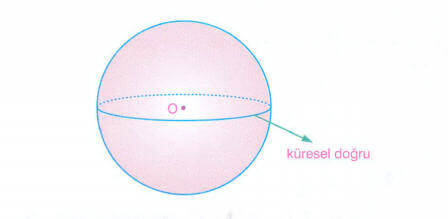
Bir küre yüzeyi ile kürenin merkezinden geçen düzlemin arakesitine küre yüzeyinin doğruları denir.
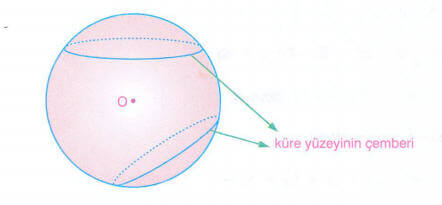
Kürenin merkezinden geçmeyen ve küre ile birden fazla noktada kesişen düzlem ile ara kesitine küre yüzeyinin çemberleri denir.
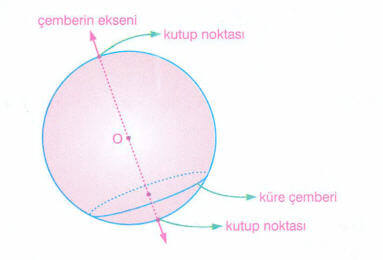
Küre yüzeyi üzerindeki bir çemberin merkezinden çıkılan dikmeye çemberin ekseni denir.
Küre yüzeyi üzerindeki bir çemberin ekseni ile küre yüzeyinin arakesit noktaları bu çemberin kutup noktalarıdır.
Küre çemberinin merkezinden geçen yarıçap doğrultusu çember düzlemine diktir. Benzer şekilde, çember düzlemine dik olan yarıçap doğrultusu çemberin merkezinden geçer.
Küre Yüzeyi İle Bir Düzlemin Konumu
XYZ dik koordinat düzleminde, bir E düzlemi ve merkezi M, yarıçapı r olan bir küre verilsin.
Küre merkezinin düzleme uzaklığı, yarıçaptan küçükse düzlem ile kürenin kesişimi bir dairedir.
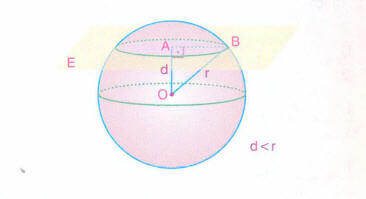
yarıçapa eşitse düzlem küre yüzeyine teğettir.
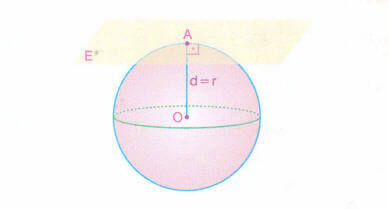
yarıçaptan büyükse düzlem küre yüzeyini kesmez.
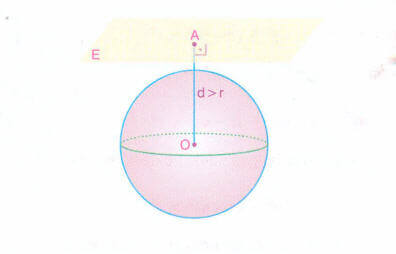
Küre Yüzeyi ile Bir Doğrunun Konumu
XYZ dik koordinat düzleminde, bir k doğrusu ve merkezi M, yarıçapı r olan bir küre verilsin.
Küre merkezinin doğruya uzaklığı, yarıçaptan küçükse doğru küre yüzeyini iki noktada keser.
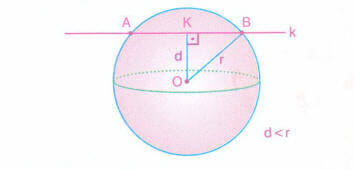
yarıçapa eşitse doğru küre yüzeyine teğettir.
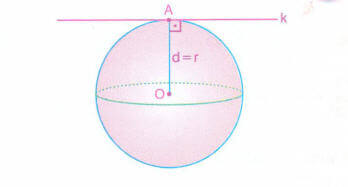
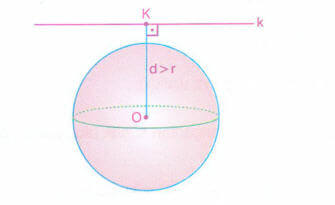
yarıçaptan büyükse doğru küre yüzeyini kesmez.
Örnek:
Uzayda, doğrusu ile,
Küresinin konumunu inceleyelim.
Çözüm:
- Kürenin merkezi olan M(5, -4, -2) noktasının doğruya uzaklığını bulalım.
- P(5, -3, 1) noktası doğru üzerinde bir nokta olmak üzere,
= M – P = (0, -1, -3) ve
- doğrunun doğrultman vektörü
= (2, 4, 3) için,
- küre merkezinin doğruya uzaklığı
olur.
olur.
birim ve
birim olduğundan,
- Kürenin yarıçapı 5 birimdir. 25 < 29 < 36 olduğundan,
olur.
- Küre merkezinin doğruya uzaklığı
yani, yarıçaptan küçük olur. Buna göre, verilen doğru küre yüzeyini iki noktada keser.