Küre Dilimi Alan ve Hacim Hesaplaması Nasıl Yapılır? Formülü Örnekler

0

By gurur on 19 Ağustos 2021 Matematik

Advertisement

Küre dilimi nedir, küre diliminin alanı ve hacmi nasıl hesaplanır? Küre dilimi alan ve hacim formülleri, örnek soru ve çözümleri.

Küre Dilimi

Bir kürenin bir çapından geçen iki yarım düzlem arasında kalan kısmına küre dilimi denir.

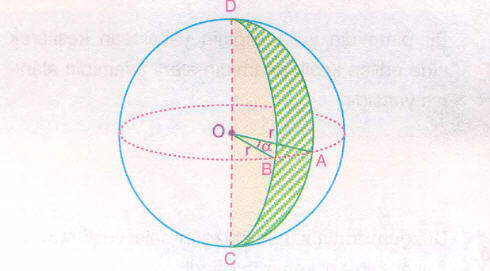
Düzlemler arasındaki merkez açının ölçüsü α ise, küre diliminin yüzey alanı,

$\displaystyle {{A}_{1}}=4\pi {{r}^{2}}\frac{\alpha }{360{}^\circ }$ eşitliğinden,
$\displaystyle {{A}_{1}}=\frac{\pi {{r}^{2}}\alpha }{90{}^\circ }$ olur.

Bu dilim, merkezinden kesilen bir karpuz dilimi gibi düşünülürse, iki yan yüzeyin alanı r yarıçaplı dairenin alanı olur.

Buna göre, küre diliminin tüm alanı,

$\displaystyle {{A}_{1}}=\frac{\pi {{r}^{2}}\alpha }{90{}^\circ }+\pi {{r}^{2}}$ olur.

Küre diliminin hacmi ise,

$\displaystyle V=\frac{4}{3}\pi {{r}^{3}}.\frac{\alpha }{360{}^\circ }$ eşitliğinden
$\displaystyle V=\pi {{r}^{3}}.\frac{\alpha }{270{}^\circ }$ olur.

Örnek:

Yarıçapı 6 cm oları bir kürenin 120° lik küre diliminin hacmini ve tüm alanını bulalım.

Çözüm:

Advertisement

120° lik merkez açısının oluşturduğu 6 cm yarıçaplı küre diliminin hacmi,
$\displaystyle V=\frac{4}{3}\pi {{r}^{3}}.\frac{\alpha }{360{}^\circ }$
$\displaystyle V=\frac{4}{3}\pi 216.\frac{120{}^\circ }{360{}^\circ }$
$\displaystyle V=\frac{4}{3}\pi 72=96\pi c{{m}^{3}}$ olur.

Alanı,

$\displaystyle S=4\pi {{r}^{2}}.\frac{\alpha }{360{}^\circ }+\pi {{r}^{2}}$
$\displaystyle S=4\pi 36.\frac{120{}^\circ }{360{}^\circ }+36\pi$
$\displaystyle S=48\pi +36\pi =84\pi c{{m}^{2}}$

Örnek:

Yarıçapı 5 cm olan küreden kesilen 36° lik dilimin hacmini bulalım.

Çözüm

Kestiğimiz dilim 36° lik olduğuna göre,
Dilimin Hacmi = $\displaystyle \frac{4}{3}\pi {{.5}^{3}}.\frac{36{}^\circ }{360{}^\circ }$
$\displaystyle =\frac{4}{3}\pi .125.\frac{1}{10}=\frac{50\pi }{3}c{{m}^{3}}$ bulunur.

Leave A Reply Cancel Reply