Paralelkenar nedir? Paralelkenarın özellikleri nelerdir? Maddeler halinde paralelkenar formülleri ve alan, çevre, köşegen, açı özellikleri.
PARALELKENAR;
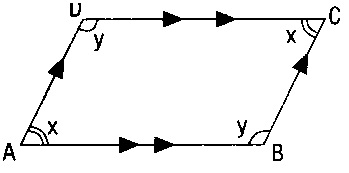
Karşılıklı kenarları paralel olan dörtgene paralelkenar denir.
- A) Karşılıklı açılan eştir.
- B) Karşılıklı kenarları eştir.
- C) Komşu açılan bütünlerdir. (x+y = 180°)
- D) Köşegenler birbirini ortalar.
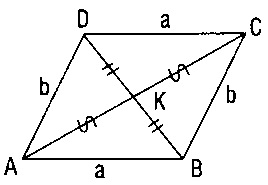
- Fakat
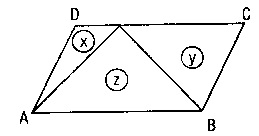
- E)
F) 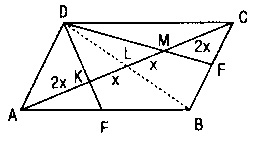
- [BC]’nin orta noktası F, [AB] nin orta noktası E ise:
G) 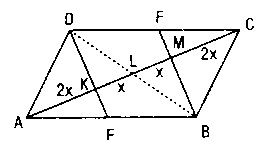
[CD] nin orta noktası F,
[AB] nin orta noktası E ise,
H) 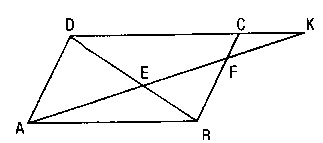
İ) 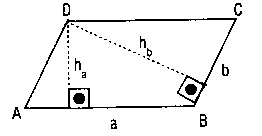
J) 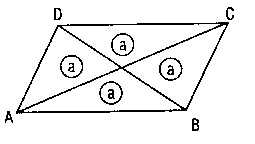
K) 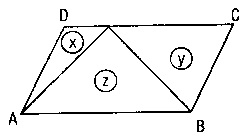
L) 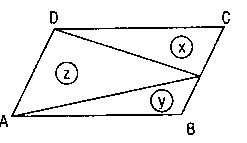
- a=b ; e=d ; c=f
M) 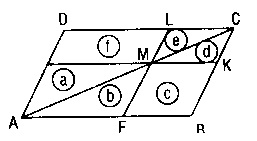
- E,F,K,L orta noktalar ise;
- A(ABCD) = 8x olur.
N) 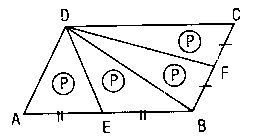
E ve F orta noktalar ise A(ABCD) = 4p’dir.
Paralelyüz Nedir? Özellikleri
Tabanları paralelkenar olan prizmaya paralelyüz denir. Şekilde, ABCD ve A’B’C’D’ tabanları paralelkenar olan prizma bir paralelyüzdür. Paralelyüzün karşılıklı yüzleri birbirine eş ve birer paralelkenardır.
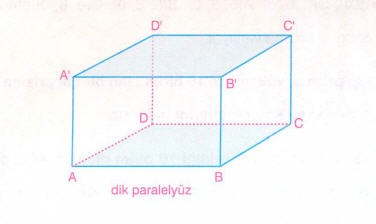
- Dik paralelyüzün tabanları paralelkenar, yan yüzleri dikdörtgendir.
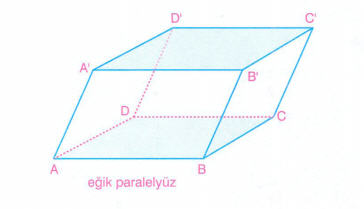
Eğik paralelyüzün yüzleri birer paralelkenardır.
PARALEL Nedir?
Birbirine kavuşmadan uzayıp giden, aralarındaki uzaklık hiç değişmeyen çizgilere geometride «paralel» (koşut) denir. Yer yuvarlağının üzerinde çizildiği tasarlanan, ekvatora koşut çemberler de bu adla anılır.
Çizgiler gibi yüzeyler de birbirine paralel olabilir. Bir çizgiyle bir yüzey arasında da paralellik bulunabilir.
İki doğru arasındaki uzaklığı göstermek için, doğrulara dik üçüncü bir doğru çizilir. Bu doğrunun, iki paralel doğru arasında kalan parçasının uzunluğu hep aynıdır.
- “Paralel”
1. Aynı düzlem içinde ikişer ikişer bulunan ve kesişmeyen, koşut, muvazi, mütevazi
“Bu, Çal Dağı’nın koyu mor sırtlarına paralel uzun ve yüce bir dağ.” – H. E. Adıvar
2. Yerküresi üzerinde çizildiği varsayılan, Ekvator’a paralel çemberlerden her biri
3. Aynı zaman içinde gelişen veya aynı özellikleri gösteren (olay, düşünce vb.) - “paralel akım ”
Bir paralel bağlantıdan geçen akım - “paralel kaidesi ”
Aynı noktaya uygulanan iki vektörün bileşkesini bulmak için her birinin bitim ucundan öbürüne paralel birer çizgi çizilerek bir paralel kenar oluşturduktan sonra vektörlerin uygulama noktasından bir köşegen çekme yolu - “paralelkenar”
Karşılıklı kenarları paralel olan dörtgen - “paralel yüz ”
Her yüzü bir paralelkenar olan biçme - “barparalel ”
Düşey direkler üzerine paralel olarak tutturulmuş iki tahta çubuktan oluşmuş jimnastik aracı