İntegral Hesaplama Yöntemleri nelerdir? Değişken değiştirme, basit kesirlere ayırma yöntemi. Kısmi (parçalı) ve trigonometrik fonksiyonların integralini alma.

İNTEGRAL HESAPLAMA YÖNTEMLERİ:
1) Değişken değiştirme (yerine koyma) yöntemi:
Her fonksiyonun integrali doğrudan formüller yardımıyla bulunmayabilir. Bu durumda integrali ∫ g(f(x)) f'(x)dx haline getirmeliyiz.
u= f(x) du= f'(x)dx alınarak
∫q(u)du integrali elde edilir. Bu integral bilinen formüllerden birine benzemelidir. Burada hangi fonksiyonun u olarak seçileceği önemlidir.
Örnek:
∫ sin³x.cosx dx =
u= sinx olsun. du=cosxdx dir.
∫ u³.du = [(u^4 )/ 4] + c = 1/4 (sin^4) x + c
2-KISMİ (PARÇALI) INTEGRAL:
Bu kesimde iki fonksiyonun çarpımından oluşan bir fonksiyonun integralinin bulunmasını inceleyeceğiz.
f ve g, bir [a,b] aralığında türevli iki fonksiyon olsunlar. Çarpım fonksiyonunun türevinden (f.g)’ = f’.g+g’.f
f.g’=(f.g)’ – f.g elde edilir.
Sürekli iki fonksiyonun çarpımı sürekli olduğundan, f.g’ (f.g)’, f’.g fonksiyonları da sürekli olduklarından integrallerebilir.
∫ f(x) . g'(x).dx = f(x) . g(x) – ∫ g(x).f'(x)dx elde edilir. f(x)=u, g(x)= v alarak Bu formül
∫ u . dv = uv – ∫ v.du biçiminde kullanılır.
Kısmî integral formülünü uygulayabilmek için verilen ifadenin iki parçaya ayrılması gerekir. Birinci parça u ile gösterilirken ikinci parça dv ile gösterilmelidir. Bu seçimyapılırken dv nin integralinden v fonksiyonu kolayca bulunmalı, ayrıca;
∫ vdu integralini hesaplamak
∫ u.dv integralini hesaplamaktan daha kolay olmalı.
3-BASİT KESİRLERE AYIRMA YÖNTEMİ:
P(x) ve Q(x) birer polinom olmak üzere P(x) /Q(x) biçimindeki fonksiyonlara rasyonel fonksiyon denilir. Burada integral alınan aralıkta Q(x) ≠ 0 olduğu kabul ediliyor. İki metot vardır.
a) Payın derecesi, paydanın derecesinden büyük veya eşit ise pay paydaya bölünür Tam kısmı ayrılır.
∫ [P(x) / Q(x)] dx = ∫ A(x) .dx + ∫ [K(x) / Q(x)] dx
Artık paydanın derecesi paydanın derecesinden küçüktür. Burada önemli olan ∫ [K(x) / Q(x)]. dx integralinin alınmasıdır.
1 Hal: Basit bir rasyonel kesrin paydası çarpanlara ayrılınca (ax+b)(cx+d)….. gibi çarpanlar ortaya çıkarsa,
(A / ax+b) + (B / cx+d) + …… şeklinde yazıp esas kesire özdeşlenerek A, B, C katsayıları bulunur.
∫ [P(x) / Q(x)] dx = ∫ [A / (x-a)] dx + ∫ [B / (x-b)] dx + ….. = A ln lx-al + B ln lx-bl + …… + c elde edilir.
II. Hal: Kesirin paydası, çarpanlara ayrılınca (ax+b)^n gibi çarpan ortaya çıkarsa bu çarpan 1’den n’ye kadar yazılır.
(A / ax+b) + (B / ax+b)² + …… + (An /ax+b)^n olur.
III Hal: Kesrin paydası çarpanlara ayrılınca daha fazla çarpanlara ayrılamayan ax² + bx + c çarpanına Ax + B
ax² + bx + c şeklinde daha basit bir kesir karşılık gelir. A, B katsayıları bulunur.
4- TRİGONOMETRİK FONKSİYONLARIN İNTEGRALİ:
Trigonometrik ifadelerin integralleri bulunurken veya bazı trigonometrik dönüşümlerin integral hesabına uygulaması yapılırken trigonometrik özdeşlikler kullanılır.
∫ Sin(ax+b) dx = -1 /a cos (ax+b)+c
∫ cos(ax+b)dx = 1 /a sin (ax+b)+c dir.
UYARI:
sinx ve cosx’in rasyonel fonksiyonlarının integrallerini alabilmek için
Tan x/2 = u dönüşümü yapılır. Bu durumda sinx’; cosx ve dx’in değerlerini bulmamız gerekir.
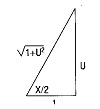
Sinx =(2u / 1+u²)cosx = (1-u²) / (1+u²)
dx = (2du / 1+u²) alınır.