Küre parçası nedir, küre parçasının yüzey alanı ve hacmi nasıl hesaplanır? Küre parçası alan ve hacim formülü, örnek soru ve çözümleri.
Matematikte, bir kürenin yüzeyine kesilmiş ve merkezi kürenin içinde kalan bölgeye “küre parçası” denir. Küre parçası, bir çemberin belirli bir açı aralığı ile kesilerek elde edilen bir 3 boyutlu cisimdir. Küre parçasının hacmini bulmak için, kürenin yarıçapı (r) ve kesilen açının (θ) bilinmesi gerekmektedir. Küre parçasının hacmi aşağıdaki formülle hesaplanır: V = (2/3) * π * r^3 * ((θ – sinθ) – (sinθ)^3)
Burada, V küre parçasının hacmi, π (pi) matematiksel sabiti, r kürenin yarıçapı ve θ kesilen açıdır.
Küre parçasının yüzey alanı hesaplanırken ise yarıçap (r) ve kesilen açının (θ) bilinmesi gerekmektedir. Küre parçasının yüzey alanı aşağıdaki formülle hesaplanır: A = 2 * π * r^2 * (1 – cos(θ/2))
Burada, A küre parçasının yüzey alanı, π (pi) matematiksel sabiti, r kürenin yarıçapı ve θ kesilen açıdır.
Küre parçasının açı aralığına bağlı olarak, kesilen bölgenin şekli değişebilir. Bu nedenle, kesilen açının büyüklüğüne ve kürenin yarıçapına bağlı olarak küre parçasının hacim ve yüzey alanı farklı değerler alabilir.
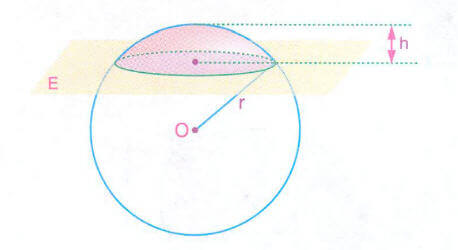
Matematikte, kürenin yüzeyine temas eden ve merkezi kürenin içinde kalan bölgeye “küre kapağı” veya “küre dilimi” denir. Küre kapağı, bir çemberin belirli bir açı aralığı ile kesilerek elde edilen bir 2 boyutlu cisimdir.
Küre kapağının alanını bulmak için, kürenin yarıçapı (r) ve kesilen açının (θ) bilinmesi gerekmektedir. Küre kapağının alanı aşağıdaki formülle hesaplanır: A = π * r^2 * (θ – sinθ)
Burada, A küre kapağının alanı, π (pi) matematiksel sabiti, r kürenin yarıçapı ve θ kesilen açıdır.
Küre kapağı, kürenin yüzeyine temas eden ve merkezi bir açı ile sınırlanan bir parçadır. Kesilen açının büyüklüğüne bağlı olarak, küre kapağı farklı şekillere sahip olabilir. Küre kapağı, kürenin yüzeyinin bir kısmını temsil eder ve kürenin diğer kısımlarından farklı özelliklere sahip olabilir.
Küre Kapağı
- Bir küre yüzeyinin bir düzlemle kesilmesi sonucu elde edilen parçalardan her birine küre kapağı denir.
- Aşağıdaki E düzlemi O merkezli küre yüzeyini iki tane küre kapağına ayırır.
- Yarıçapı r olan kürede, yüksekliği h olan küre kapağının alanı,
Yarıçapı r olan kürede, yüksekliği h olan küre parçasının hacmi, olur.
Örnek:
Bir küre merkezinden 4 cm uzaklıktaki bir düzlemle kesiliyor. Kesit alanı 9π cm² olduğuna göre,
- a. küre kapağının alanını bulalım.
- b. küre parçasının hacmini bulalım.
Çözüm
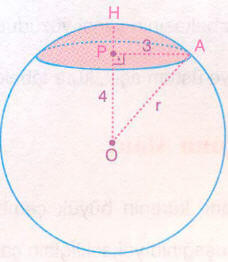
Düzlemle kürenin kesit alanı,
- 9π cm² olduğundan,
- kesitin yarıçapı, |AP| = 3 cm olur.
- OAP (3-4-5) dik üçgeni olduğundan,
- r = |OA| = 5 cm olur.
- |OH| = r = 5 cm olduğundan,
- küre kapağının yüksekliği |PH| = h = 5- 4 = 1cm olur.
Buna göre,
- a. Küre Kapağının Alanı =
bulunur. - b. r = 5 cm ve h = 1 cm için küre parçasının hacmi,
olur.
Küre Tabakasının Hacmi
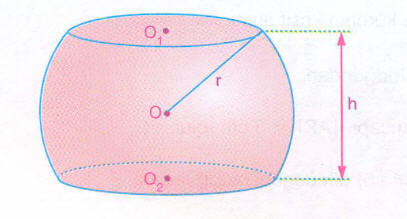
Küre tabakasının hacmini bulmak için, kürenin yarıçapı (r), iç açı (α) ve dış açı (β) bilgilerine ihtiyaç vardır. İç açı, küre tabakasının merkezindeki açıyı temsil ederken, dış açı ise küre tabakasının kenarında yer alan açıyı ifade eder. Küre tabakasının hacmi aşağıdaki formülle hesaplanır: V = (2/3) * π * r^3 * (β – sin(β) – (α – sin(α)))
Burada, V küre tabakasının hacmi, π (pi) matematiksel sabiti, r kürenin yarıçapı, α iç açı ve β dış açıdır.
Küre tabakasının hacmi, iç açı ve dış açıya bağlı olarak değişir. Ayrıca, kürenin yarıçapı da hacim hesaplamasında önemli bir faktördür. İç açı ve dış açı arasındaki fark ne kadar büyük olursa, küre tabakasının hacmi de o kadar büyük olur.
Örnek
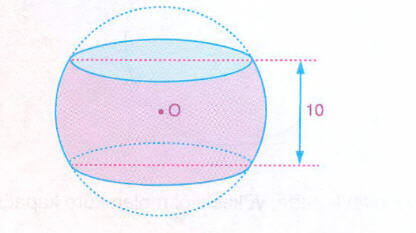
Yarıçapının uzunluğu 12 cm olan bir küre, merkezine uzaklığı 5 cm olan paralel iki düzlemle kesiliyor. Buna göre, paralel iki düzlem arasında kalan
- a. küre kuşağının alanını bulalım.
- b. küre tabakasının hacmini bulalım.
Çözüm
Küre merkezinden 5 cm uzaklıkta iki düzlem çizilebilir. Bu durumda paralel iki düzlem arasındaki uzaklık 10 cm olur.
- Küre Kuşağının Alanı =
- Küre Kuşağının Alanı =
- Küre Kuşağının Alanı = 240 π cm² olur.
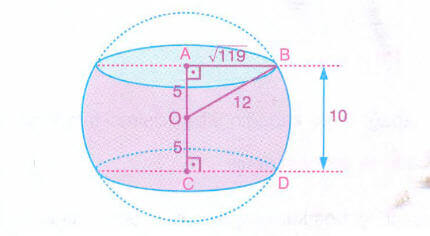
Şekilde, düzlemlerin küre merkezine uzaklığı 5 cm ve r = 12 cm olduğundan, AOB dik üçgeninde pisagor bağıntısından,
- a = |AB| =
cm,
- b = |CD| =
cm olur.
Buna göre küre tabakasının hacmi,
cm³ olur.