İki kümenin farkı ve iki kümenin simetrik farkı nedir? İki kümenin farkı ile ilgili özellikler ve örnek soru ve çözümü.
İki kümenin farkı, birinci kümenin elemanlarından ikinci kümenin elemanları çıkarıldığında kalan elemanların toplamıdır. Örneğin, {1, 2, 3} ve {2, 3, 4} kümelerinin farkı, {1} kümesidir.
Simetrik fark, iki kümenin farkının simetrisidir. Örneğin, {1, 2, 3} ve {2, 3, 4} kümelerinin simetrik farkı, {1, 4} kümesidir. Simetrik fark, iki kümenin elemanlarının birbirlerinden çıkarılmasıyla elde edilir. Örneğin, {1, 2, 3} ve {2, 3, 4} kümelerinin simetrik farkı, {1, 4} kümesidir. Simetrik fark, aşağıdaki şekilde gösterilebilir:
(A – B) ∪ (B – A) = (A ∪ B) – (A ∩ B)
Bu eşitlik, iki kümenin simetrik farkını, iki kümenin birleşimi (A ∪ B) ve kesişimleri (A ∩ B) çıkarılarak bulunabileceğini gösterir.
Simetrik fark, genellikle A ve B kümelerinin farkını bulmak için kullanılır, ancak birleşim ve kesişimleri de içeren bir ifade olarak da kullanılabilir. İki kümenin farkı, birinci kümenin elemanlarından ikinci kümenin elemanlarını çıkarıldığında kalan elemanların toplamıdır. Örneğin, {1, 2, 3} ve {2, 3, 4} kümelerinin farkı, {1} kümesidir.
Fark işleminin matematiksel gösterimi aşağıdaki gibi olur:
A – B = {x | x ∈ A ve x ∉ B}
Bu ifade, A kümesinin elemanlarından B kümesinin elemanlarını çıkararak kalan elemanların toplamını gösterir.
Simetrik fark ise, iki kümenin farkının simetrisidir. Örneğin, {1, 2, 3} ve {2, 3, 4} kümelerinin simetrik farkı, {1, 4} kümesidir. Simetrik fark, aşağıdaki şekilde gösterilebilir:
(A – B) ∪ (B – A) = (A ∪ B) – (A ∩ B)
Bu eşitlik, iki kümenin simetrik farkını, iki kümenin birleşimi (A ∪ B) ve kesişimleri (A ∩ B) çıkarılarak bulunabileceğini gösterir. Simetrik fark, genellikle A ve B kümelerinin farkını bulmak için kullanılır, ancak birleşim ve kesişimleri de içeren bir ifade olarak da kullanılabilir.
İki Kümenin Farkı:
A ve B iki küme olsun. A da bulunup B de bulunmayan elemanların kümesine A ile B nin farkı denir. A\B şeklinde gösterilir. A\B= {xl x∈ A ve x ∉ B} olur. Venn şeması ile gösterilir ise:
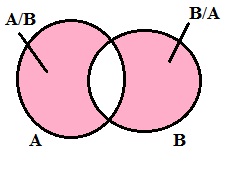
Simetrik fark:
(A\B) ∪ (B\A)’ya simetrik fark denir. Not: Bir A kümesinin bütün alt kümelerinin kümesine A’nın kuvvet kümesi denir.
Örnek Soru ve Çözümü
Örneğin, {1, 2, 3, 4} ve {3, 4, 5, 6} kümelerinin farkını bulalım.
A kümesi: {1, 2, 3, 4}
B kümesi: {3, 4, 5, 6}
A – B = {x | x ∈ A ve x ∉ B}
Bu ifadeye göre, A kümesinin elemanlarından B kümesinin elemanlarını çıkararak kalan elemanların toplamını bulacağız.
Bunun anlamı, A kümesinin elemanlarından B kümesinin elemanlarını çıkararak kalan elemanların toplamını bulacağız. Bu durumda, A kümesinin elemanları {1, 2, 3, 4} ve B kümesinin elemanları {3, 4, 5, 6} olduğundan, A – B = {1, 2} olur.
Bu nedenle, {1, 2, 3, 4} ve {3, 4, 5, 6} kümelerinin farkı, {1, 2} kümesidir.