Logaritma fonksiyonu nedir? Matematik dünyasında önemli bir yere sahip olan logaritma fonksiyonunu detaylı bir şekilde açıklıyoruz. Logaritma fonksiyonunun temel özelliklerini öğrenirken, gerçek dünya uygulamalarını da keşfedeceksiniz.
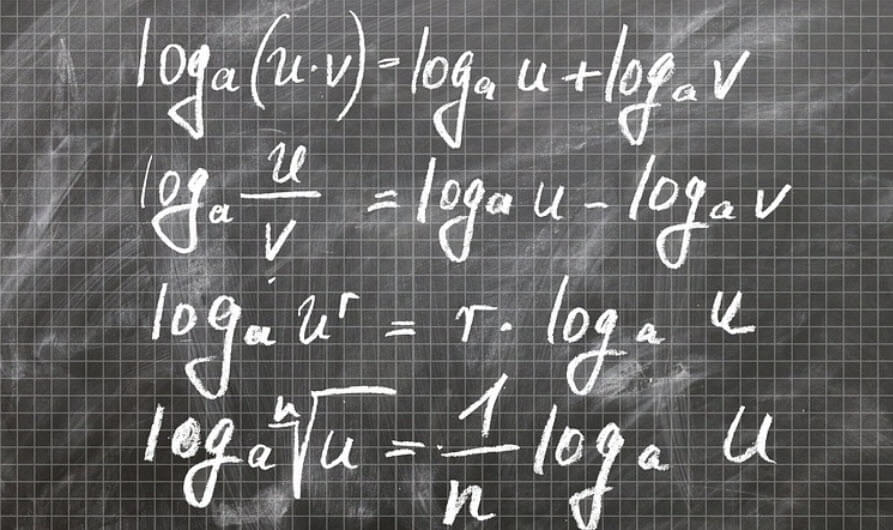
Kaynak: pixabay.com
Logaritma, matematikte bir sayının başka bir sayıya göre üs olduğunu ifade eden bir işlemdir. İki sayı arasındaki ilişkiyi açığa çıkarmak için kullanılır. Genellikle “log” şeklinde kısaltılan logaritma, bir taban sayısı üzerinden hesaplanır. Örneğin, logaritmanın tabanı 10 ise, logaritma işlemini log10 şeklinde gösteririz. Aynı şekilde, logaritmanın tabanı e sayısı (yaklaşık olarak 2.71828) ise, doğal logaritma olarak adlandırılır ve ln(x) şeklinde gösterilir.
Logaritma fonksiyonunun temel özelliği, bir sayının logaritmasının, o sayının hangi üsle taban sayısına yükseltildiğiyle ifade edilebileceğidir. Yani, a^b = c ise, loga(c) = b şeklinde ifade edilebilir. Bu denklemde, a tabanı, b üsü ve c ise sonucu temsil eder. Logaritma fonksiyonunun bazı önemli özellikleri şunlardır:
- Logaritma tabanı pozitif bir sayı olmalıdır. Logaritma fonksiyonunun tanım kümesi, taban sayısının pozitif olduğu tüm gerçek sayılardır.
- Logaritma fonksiyonu, yalnızca pozitif reel sayılar üzerinde tanımlıdır. Negatif veya sıfır değerler için logaritma işlemi tanımsızdır.
- Logaritma fonksiyonunun grafiği, taban sayısının artışına bağlı olarak yavaş yavaş artar. Logaritmanın tabanı 1’den büyükse, fonksiyon pozitif değerler için artan bir eğime sahiptir. Logaritmanın tabanı 1’den küçükse, fonksiyon negatif değerler için azalan bir eğime sahiptir.
- Logaritma fonksiyonu, çeşitli matematiksel problemlerin çözümünde kullanılır. Özellikle büyük sayılarla çalışırken ve üstel büyüme hızını hesaplarken logaritma fonksiyonu önemli bir araçtır.
- Logaritma fonksiyonu, tersi olan üssel fonksiyon ile de ilgilidir. İki fonksiyon birbirinin tersidir ve birbirlerini iptal ederler. Yani, loga(a^b) = b ve a^(loga(x)) = x eşitlikleri geçerlidir.
Bu temel bilgiler logaritma fonksiyonu hakkında genel bir anlayış sağlamaktadır.
2ˣ ve log₂(x) Arasındaki Grafiksel İlişki
2^x ve log₂(x) fonksiyonları arasında grafiksel bir ilişki bulunmaktadır. İki fonksiyonun grafikleri, birbirinin yansımasıdır.
- 2^x Fonksiyonu: 2^x fonksiyonu, üstel bir fonksiyon olarak adlandırılır. Tabanı 2 olan bu fonksiyonda, x her arttığında fonksiyonun değeri iki katına çıkar. Yani, x arttıkça fonksiyon hızla büyür.Örneğin, x = 0 olduğunda 2^0 = 1 olur. x = 1 olduğunda 2^1 = 2, x = 2 olduğunda 2^2 = 4 olur ve böylece devam eder. Fonksiyon sürekli bir şekilde artar.2^x fonksiyonunun grafiği, y ekseni üzerinde sıfır noktasından başlar ve pozitif yönünde sonsuza doğru genişler. Eğimi x’in artış hızına bağlı olarak hızla artar.
- log₂(x) Fonksiyonu: log₂(x) fonksiyonu, logaritmanın tabanı 2 olan bir fonksiyondur. Bu fonksiyon, x’in hangi üsle 2’ye eşit olduğunu ifade eder. Yani, 2^y = x ise, log₂(x) = y olur.Örneğin, log₂(1) = 0, log₂(2) = 1, log₂(4) = 2 gibi değerlere sahiptir. Fonksiyon x değeri arttıkça yavaşça büyür.log₂(x) fonksiyonunun grafiği, x ekseni üzerinde 1’den başlar ve pozitif yönünde sonsuza doğru genişler. Ancak, fonksiyonun eğimi x’in artış hızıyla birlikte yavaşça azalır.
Grafiksel olarak, 2^x fonksiyonunun grafiği y = log₂(x) fonksiyonunun grafiği üzerine yansır. Yani, herhangi bir noktadaki x ve y değerleri, diğer fonksiyonun grafiğinde simetrik bir noktayı temsil eder.
Örneğin, 2^1 = 2 ve log₂(2) = 1 olduğunu düşünelim. Bu noktada, (1, 2) koordinatları 2^x fonksiyonunun grafiğinde bulunan bir noktaya, ve (2, 1) koordinatları ise log₂(x) fonksiyonunun grafiğinde bulunan bir noktaya karşılık gelir. Bu şekilde, 2^x fonksiyonu ve log₂(x) fonksiyonu arasında grafiksel bir ilişki bulunmaktadır.
Logaritmik Fonksiyonların Grafikleri Konu Anlatımı ve Çizimi
Logaritmik fonksiyonlar, matematikte logaritmanın farklı tabanlar üzerinden hesaplandığı fonksiyonlardır. İki yaygın logaritmik fonksiyon, doğal logaritma (ln(x)) ve ondalık logaritma (log₁₀(x)) fonksiyonlarıdır.
Doğal Logaritma (ln(x)): Doğal logaritma, logaritmanın tabanının e sayısı (yaklaşık olarak 2.71828) olduğu bir fonksiyondur. ln(x) şeklinde gösterilir. Doğal logaritma fonksiyonunun grafik özelliklerine bakalım:
- Alan: ln(x) fonksiyonu yalnızca pozitif gerçek sayılar üzerinde tanımlıdır. ln(x)’in tanım kümesi (0, +∞) aralığıdır.
- Asimptotlar: ln(x) fonksiyonunun grafiği, x eksenine yaklaştıkça asimptotik bir davranış sergiler. Yani, ln(x)’in grafiği x ekseni ile sınırlı olup, x ekseniyle hiçbir zaman kesişmez.
- Artış Hızı: ln(x) fonksiyonu, x değeri arttıkça artan bir eğime sahiptir. Ancak, artış hızı x büyüdükçe yavaşlar.
- İvme: ln(x) fonksiyonunun grafiği, x değeri büyüdükçe ivmesi azalır. Yani, eğimin artış hızı azalır.
Ondalık Logaritma (log₁₀(x)): Ondalık logaritma, logaritmanın tabanının 10 olduğu bir fonksiyondur. log₁₀(x) şeklinde gösterilir. Ondalık logaritma fonksiyonunun grafik özelliklerine göz atalım:
- Alan: log₁₀(x) fonksiyonu yalnızca pozitif gerçek sayılar üzerinde tanımlıdır. log₁₀(x)’in tanım kümesi (0, +∞) aralığıdır.
- Asimptotlar: log₁₀(x) fonksiyonunun grafiği, x eksenine yaklaştıkça asimptotik bir davranış sergiler. Yani, log₁₀(x)’in grafiği x ekseniyle hiçbir zaman kesişmez.
- Artış Hızı: log₁₀(x) fonksiyonu, x değeri arttıkça artan bir eğime sahiptir. Ancak, artış hızı x büyüdükçe yavaşlar.
- İvme: log₁₀(x) fonksiyonunun grafiği, x değeri büyüdükçe ivmesi azalır. Yani, eğimin artış hızı azalır.
Logaritmik fonksiyonların grafiklerini çizmek için aşağıdaki adımları takip edebilirsiniz:
- İlk adım, çizmek istediğiniz logaritmik fonksiyonun tanım kümesini belirlemektir. Logaritmik fonksiyonlar genellikle pozitif gerçek sayılar üzerinde tanımlıdır. Örneğin, ln(x) fonksiyonu için x > 0 ve log₁₀(x) fonksiyonu için x > 0 olmalıdır.
- İkinci adım, fonksiyonun değerlerini hesaplamak ve bir veri tablosu oluşturmaktır. Bunun için çeşitli x değerleri seçebilir ve bu x değerlerine karşılık gelen y değerlerini hesaplayabilirsiniz. Örneğin, ln(x) fonksiyonu için farklı x değerleri seçebilir ve bu değerlere karşılık gelen ln(x) değerlerini hesaplayabilirsiniz.
- Üçüncü adım, veri tablosundaki noktaları bir koordinat düzleminde işaretlemektir. x değerlerini x ekseni üzerinde ve y değerlerini y ekseni üzerinde işaretleyin.
- Dördüncü adım, noktaları birleştirerek fonksiyonun grafiğini çizmektir. İşaretlediğiniz noktaları birleştiren pürüzsüz bir eğri çizin. Eğer elde ettiğiniz noktalar düz bir çizgiye yakınsıyorsa, grafik bir doğru olabilir. Aksi takdirde, eğri bir çizgi veya kavisli bir çizgi olabilir.
- Grafikteki asimptotları belirleyin. Asimptotlar, fonksiyonun grafiğine yaklaştığı ancak hiçbir zaman kesilmediği yatay veya dikey çizgilerdir. ln(x) fonksiyonu için x ekseniyle hiçbir zaman kesişmeyen yatay bir asimptot vardır. log₁₀(x) fonksiyonu için de x ekseniyle hiçbir zaman kesişmeyen yatay bir asimptot bulunur.
Bu adımları takip ederek logaritmik fonksiyonların grafiklerini çizebilirsiniz. Ancak, logaritmik fonksiyonların grafikleri diğer fonksiyonlardan farklı özelliklere sahip olabilir, bu nedenle dikkatli bir şekilde çizmek önemlidir. Ayrıca, grafik çiziminde bir hesap makinesi veya matematik yazılımı kullanabilirsiniz, çünkü bu programlar fonksiyonun değerlerini hızlı ve doğru bir şekilde hesaplayabilir.
Logaritmik Ölçek
Logaritmik ölçek, bir veri setini veya grafiksel bir gösterimi logaritmik bir skalaya dönüştürmeyi ifade eder. Bu tür bir ölçek kullanılarak, büyük sayıların ve geniş aralıkların daha kolay ve daha anlaşılır bir şekilde temsil edilebileceği bir grafik elde edilebilir.
Logaritmik ölçeği anlamak için öncelikle lineer ölçeği anlamak önemlidir. Lineer ölçekte, her birim aralığı eşit olarak ölçeklenir. Örneğin, x ekseni üzerinde 1, 2, 3, 4 gibi ardışık tam sayılar olsun. Bu durumda, iki ardışık sayı arasındaki mesafe her zaman aynıdır.
Ancak logaritmik ölçekte, her birim aralığı eşit olarak ölçeklenmez. Logaritmik ölçekte, her birim aralığına karşılık gelen değerler, tabanın logaritması alınarak belirlenir. Örneğin, logaritmik ölçekte 1, 10, 100, 1000 gibi ardışık sayılar olsun. Bu durumda, iki ardışık sayı arasındaki mesafe değişir. Örneğin, 10 ile 100 arasındaki mesafe 90 birimken, 100 ile 1000 arasındaki mesafe 900 birim olacaktır.
Logaritmik ölçeğin kullanımı, özellikle büyük sayılar veya geniş aralıklarla çalışırken faydalıdır. Örneğin, bilimsel verilerde veya finansal grafiklerde logaritmik ölçek sıklıkla kullanılır. Bu tür verilerde, büyük değerler ve aralıklar, logaritmik ölçekle daha iyi görselleştirilebilir ve anlaşılabilir hale gelir.
Logaritmik ölçekte grafik çizmek için, önce kullanacağınız tabanı belirlemeniz gerekmektedir. Örneğin, logaritmik ölçekte taban 10 kullanıyorsanız, değerleri log₁₀(x) şeklinde hesaplayabilirsiniz. Ardından, elde ettiğiniz değerleri bir veri tablosunda kaydedebilir ve bu değerlerle grafik çizebilirsiniz. Grafikteki birim mesafeler logaritmik olarak artacaktır.
Logaritmik ölçek, büyük sayıların ve geniş aralıkların daha anlaşılır bir şekilde temsil edilmesine yardımcı olan önemli bir araçtır. Ancak, logaritmik ölçeği anlamak ve kullanmak için pratik yapmanız ve alışmanız gerekebilir.
Toplama ve çıkarma işlemlerinde kullanabileceğimiz logaritma özdeşlikleri
Logaritma özdeşlikleri, logaritmaların toplama ve çıkarma işlemlerinde nasıl kullanılabileceğini gösteren matematiksel ilişkilerdir. Aşağıda, toplama ve çıkarma işlemlerinde kullanılabilecek bazı logaritma özdeşliklerini bulabilirsiniz:
- Logaritmanın Çarpma Özdeşliği: loga(xy) = loga(x) + loga(y) Bu özdeşlik, logaritmanın çarpma işlemi üzerinde nasıl etkili olduğunu gösterir. Çarpanları ayrı ayrı logaritmalayıp topladığınızda, sonuç, çarpımın logaritmasıyla aynıdır.
- Logaritmanın Bölme Özdeşliği: loga(x/y) = loga(x) – loga(y) Bu özdeşlik, logaritmanın bölme işlemi üzerinde nasıl etkili olduğunu gösterir. Bölünen ve böleni ayrı ayrı logaritmalayıp çıkardığınızda, sonuç, bölümün logaritmasıyla aynıdır.
- Logaritmanın Üs Özdeşliği: loga(x^n) = n * loga(x) Bu özdeşlik, logaritmanın üs alma işlemi üzerinde nasıl etkili olduğunu gösterir. Bir sayının üssünü alıp sonra logaritmaladığınızda, sonuç, üssünü aldığınız sayının logaritmasının o üssüyle çarpımına eşittir.
Bu özdeşlikler, logaritmaları kullanarak toplama ve çıkarma işlemlerini daha kolay hale getirir ve bazen karmaşık hesaplamaları basitleştirir. Logaritma özdeşliklerini kullanarak logaritmaların toplama ve çıkarma işlemlerini daha verimli bir şekilde gerçekleştirebilirsiniz. Ancak, özdeşlikleri doğru uyguladığınızdan ve ilgili logaritma tabanını doğru şekilde belirlediğinizden emin olmalısınız.
Bir logaritmanın bir sabitle çarpımı için kullanabileceğimiz logaritma özdeşliklerini ve taban değiştirme kuralı
Bir logaritmanın bir sabitle çarpımını hesaplamak için kullanabileceğiniz birkaç logaritma özdeşliği ve taban değiştirme kuralı vardır. İşte bunlardan bazıları:
- Sabit Çarpan Özdeşliği: loga(c * x) = loga(c) + loga(x) Bu özdeşlik, bir logaritmanın bir sabitle çarpımını hesaplarken kullanılabilir. Sabit çarpanın logaritması, sabitin logaritmasının çarpanla toplamına eşittir.
- Taban Değiştirme Kuralı: loga(x) = logb(x) / logb(a) Bu kural, bir logaritmanın tabanını değiştirmek için kullanılır. Örneğin, log₃(x)’i log₁₀(x) olarak ifade etmek istiyorsanız, logaritmanın tabanını değiştirmek için logb(a) ifadesini kullanarak bu dönüşümü yapabilirsiniz. Burada b, hedef tabanı temsil eder.
- Özel Durum: Doğal Logaritma (ln) ile Taban Değiştirme: ln(x) = loge(x) Doğal logaritma (ln), tabanı e (Euler sayısı) olan bir logaritmik fonksiyondur. Eğer doğal logaritmayı (ln) başka bir tabana dönüştürmek isterseniz, yukarıda bahsedilen taban değiştirme kuralını kullanabilirsiniz. Örneğin, ln(x)’i log₁₀(x) olarak ifade etmek için: ln(x) = loge(x) = log₁₀(x) / log₁₀(e) kullanılabilir.
Bu özdeşlikler ve taban değiştirme kuralı, logaritma hesaplamalarını basitleştirmek ve farklı tabanlarda logaritma ifadeleri arasında dönüşüm yapmak için kullanılır. Logaritma işlemleri sırasında doğru tabanı ve doğru özdeşliği kullanmaya özen göstermek önemlidir.
Logaritmada Çarpım Kuralı
Logaritmada çarpım kuralı, logaritmaların çarpma işleminde nasıl etkili olduğunu ifade eden bir matematiksel kuraldır. Logaritmada çarpım kuralı şu şekildedir:
logₐ(xy) = logₐ(x) + logₐ(y)
Bu kurala göre, iki sayının çarpımının logaritması, bu sayıların logaritmalarının toplamına eşittir. Burada logₐ ifadesi, tabanı a olan logaritmayı temsil eder.
Bu kural, çarpma işlemi içeren logaritmaları daha basit bir şekilde hesaplamamızı sağlar. Örneğin, log₃(4 * 5) hesaplamak istediğimizi düşünelim. Bu durumda, log₃(4) ve log₃(5) değerlerini hesaplayıp ardından bu değerleri toplarız:
log₃(4 * 5) = log₃(4) + log₃(5)
Sonuç olarak, log₃(4 * 5) değeri, log₃(4) + log₃(5) şeklinde ifade edilir.
Logaritmada çarpım kuralı, logaritmaların çarpma işlemlerini daha kolay hale getirir ve hesaplamaları basitleştirir. Bu kuralı kullanarak logaritma ifadelerini toplayabilir ve çarpma işlemlerini daha verimli bir şekilde gerçekleştirebilirsiniz.