Son Yazılar :
NKFUCOM
NKFUCOM

Üçgenlerin Benzerlik Teoremleri

0
By on Bilgi Dünyası

Üçgenlerin bezerliği, açı-açı, kenar-açı ve kenar-kenar benzerlik teoremleri, formülleri ve çizimli açıklamaları.

ÜÇGENLERİN BENZERLİĞİ

ABC, DEF üçgenlerinin köşeleri arasında bir eşleme verilmiş olsun. \displaystyle \left( \overset{\Delta }{\mathop{ABC}}\,\overset{{}}{\mathop{\Leftrightarrow \overset{\Delta }{\mathop{DEF}}\,}}\, \right) bu iki üçgende karşılıklı açılar eş ise bu iki üçgen benzerdir denir.

BENZERLİK TEOREMLERİ

1. Açı, Açı Benzerlik Teoremi:

İkişer açılan eşit olan üçgenler benzerdir.

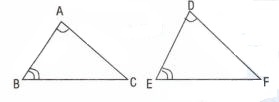
aci-aci-benzerlik,

\displaystyle m\hat{A}=m\hat{D} VE \displaystyle m\hat{B}=m\hat{E}

ise

\displaystyle \overset{\Delta }{\mathop ABC}\,\sim \overset{\Delta }{\mathop DEF}\,

2. Kenar, Açı, Kenar Benzerlik Teoremi:

İkişer kenarları orantılı ve kenarlar arasındaki açılar eşit olan üçgenler benzerdir.

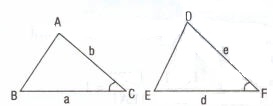
kenar-aci-benzerlik

\displaystyle \frac{a}{d}=\frac{b}{e}

ve

\displaystyle m\hat{C}=m\hat{F}

ise

\displaystyle \overset{\Delta }{\mathop ABC}\,\sim \overset{\Delta }{\mathop DEF}\,

3. Kenar, Kenar, Kenar Benzerlik Teoremi;

Üçer kenarları orantılı olan üçgenler benzerdir.

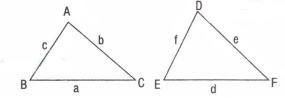
kenar-kenar-benzerlik

\displaystyle \frac{a}{d}=\frac{b}{e}=\frac{c}{f}

ise

\displaystyle \overset{\Delta }{\mathop ABC}\,\sim \overset{\Delta }{\mathop DEF}\,

SONUÇLAR:

\displaystyle \frac{a}{d}=\frac{b}{e}=\frac{c}{f} ise

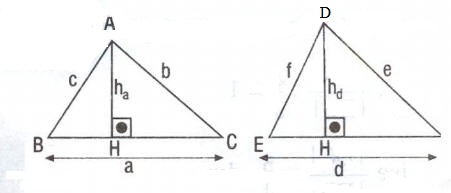
ucgen-kenar-benzerlik

\displaystyle 1)\frac{a}{d}=\frac{b}{e}=\frac{c}{f}=k

k benzerlik oranıdır.

\displaystyle 2)\frac{{{h}_{a}}}{{{h}_{d}}}=\frac{{{h}_{b}}}{{{h}_{e}}}=\frac{{{h}_{c}}}{{{h}_{f}}}=k

\displaystyle 3)\frac{{{V}_{a}}}{{{V}_{d}}}=\frac{{{V}_{b}}}{{{V}_{e}}}=\frac{{{V}_{c}}}{{{V}_{f}}}=k

\displaystyle 4)\frac{{{n}_{A}}}{{{n}_{D}}}=\frac{{{n}_{B}}}{{{n}_{E}}}=\frac{{{n}_{C}}}{{{n}_{F}}}=k

2,3,4 oranlarım sözle ifade edecek olursak, Benzer üçgenlerin yükseklikleri, kenar ortayları ve açı ortayları oranı benzerlik oranına eşittir.

5) ABC, DEF üçgenlerinin iç teğet çemberinin yarı çapları r, r’ ve çevrel çemberlerinin yarıçapları R, R’ ise

\displaystyle \frac{r}{r'}=k

\displaystyle \frac{R}{R'}=k dır.

\displaystyle 6)A\left( \overset{\Delta }{\mathop ABC}\, \right)=S

ve

\displaystyle A\left( \overset{\Delta }{\mathop DEF}\, \right)=S'

ise

\displaystyle \frac{S}{S'}={{k}^{2}} dir.


Leave A Reply