Son Yazılar :
NKFUCOM
NKFUCOM

Açıortay Teoremi ve İspatı

0
By on Bilgi Dünyası
Advertisement

Üçgende açıortay teoremi nedir? Üçgende açıortay teoreminin formülü, hesaplanması ve ispatı.

AÇIORTAY TEOREMİ

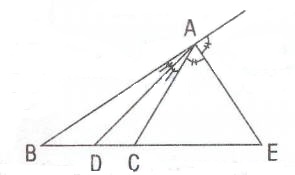
aciortay-teoremi

ABC üçgeninde [AD], [AE] sırası ile A açısının iç ve dış açı ortayları ise

\displaystyle \frac{\left| DB \right|}{\left| DC \right|}=\frac{\left| AB \right|}{\left| AC \right|}=\frac{\left| EB \right|}{\left| EC \right|}

İSPAT

Advertisement

aciortay-teoremi-ispat

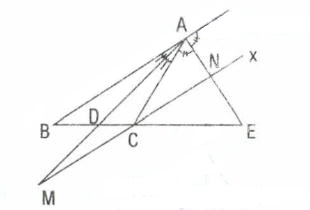
C köşesinden \displaystyle \left[ AB \right]\parallel [CX çizelim. Çizilen paralel [AD] yi M, [AE] yi N de kessin.

\displaystyle m\left( \overset\frown{BAD} \right)=m\left( \overset\frown{DAC} \right)

[AD] açıortay, MCA üçgeni ikizkenardır.

\displaystyle \left| MC \right|=\left| AC \right|

\displaystyle \frac{\left| BD \right|}{\left| DC \right|}=\frac{\left| AB \right|}{\left| MC \right|}\left[ MC \right]\parallel \left[ AB \right]

Advertisement

olduğundan \displaystyle \left| MC \right| nin eşiti yerine yazılırsa,

\displaystyle \frac{\left| DB \right|}{\left| DC \right|}=\frac{\left| AB \right|}{\left| AC \right|}\to \left( 1 \right)

bulunur.

\displaystyle m\left( \overset\frown{ACN} \right)=m\left( \overset\frown{BAC} \right) iç ters

\displaystyle m\left( \overset\frown{CAN} \right)=m\left( \frac{\hat{B}+\hat{C}}{2} \right) [AE] dış açıortay

\displaystyle m\left( \overset\frown{CNA} \right)=180{}^\circ -m\left( A+\frac{B+C}{2} \right)=m\left( \frac{B+C}{2} \right)

ACN üçgeni ikizkenar \displaystyle \left| AC \right|=\left| CN \right|

\displaystyle \frac{\left| EB \right|}{\left| EC \right|}=\frac{\left| AB \right|}{\left| CN \right|}

\displaystyle \left[ CN \right]\parallel \left[ AB \right] olduğundan

\displaystyle \left| CN \right| nin eşiti yerine yazılırsa,

\displaystyle \frac{\left| EB \right|}{\left| EC \right|}=\frac{\left| AB \right|}{\left| AC \right|}\to \left( 2 \right) bulunur.

Advertisement

(1) ve (2) eşitliklerinden,

\displaystyle \frac{\left| DB \right|}{\left| DC \right|}=\frac{\left| AB \right|}{\left| AC \right|}=\frac{\left| EB \right|}{\left| EC \right|} bulunur.

İç ve dış açıortayların uzunlukları ise üçgenin kenar uzunlukları a, b, c olmak üzere;

\displaystyle \left| AD \right|=\sqrt{b.c-\left| DB \right|.\left| DC \right|}

\displaystyle \left| AE \right|=\sqrt{\left| EB \right|.\left| EC \right|-b.c}

bağıntıları bulunur.


Leave A Reply