Çarpım sembolü nasıldır, matematikte nasıl kullanılır? Çarpım özellikleri, önemli formülleri, çarpım sembolü, büyük harf pi hakkında bilgi.
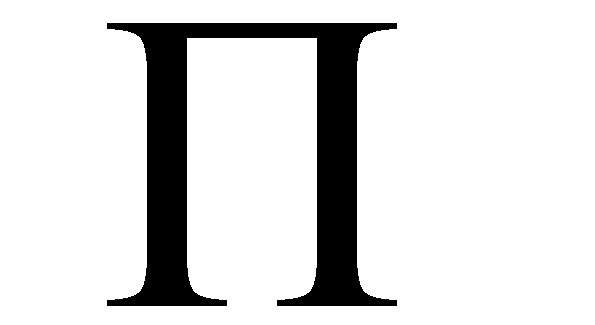
ÇARPIM (∏)
∀k∈N+için ak∈R olmak üzere;
ÇARPIM ÖZELLİKLERİ
Büyük Harf Pi
Matematiksel çarpım için farklı bir kod noktası (∏) bulunmasına rağmen, büyük harf pi sembolü kolaylık sağlamak için kullanılmaya devam etmektedir.
Dizi Çarpımları
Büyük harf pi sembolü
Bir dizi faktörün çarpımı, Yunan alfabesindeki büyük harf Π (pi) ‘den türeyen çarpım simgesiyle yazılabilir. Unicode U + 220F (∏) konumu, U + 03A0 (Π) harfinden farklı olarak böyle bir çarpımı belirtmek için bir kabartma içerir. Bu gösterimin anlamı şu şekilde verilir:
Alt simge, alt sınırı (1) ile birlikte “çarpma indeksi” olarak adlandırılan bağlı değişkenin (bu durumda i) sembolünü verirken, üst simge (burada 4) üst sınırını verir. Alt ve üst sınır, tamsayıları ifade eden ifadelerdir. Çarpımın faktörleri, çarpma indisi için ikame edilen ardışık tamsayı değerleri ile alt sınırdan başlayarak ve 1 ila üst sınır dahil olmak üzere arttırarak çarpım operatörünü takip eden ifadenin alınmasıyla elde edilir. Yani mesela:
Daha genel olarak, gösterim şu şekilde tanımlanır:
burada m ve n tamsayı veya tamsayı olarak değerlendirilen ifadelerdir. M = n olması durumunda, çarpımın değeri tekli faktör xm ile aynıdır. M > n ise, çarpım, faktörlerin ifadesine bakılmaksızın değeri 1 olan boş bir çarpımdır.
Sonsuz çarpımlar
Ayrıca, sonsuz sayıda terim olan çarpımlar da düşünülebilir; bunlara sonsuz çarpımlar denir. İşaretlemede, yukarıdaki n’yi sonsuz işareti (∞) ile değiştiririz. Böyle bir serinin çarpımı, n sınırsız büyüdükçe ilk n terimin çarpımın sınırı olarak tanımlanır. Yani, tanım gereği,
Benzer şekilde, m negatif sonsuz ile değiştirilebilir ve şu şekilde tanımlanabilir:
her iki sınır da mevcuttur.